Chapter 4-2. 기초 베이지안 통계
베이지안 통계학은 딥 러닝의 여러 분야에서 사용된다. 대표적인 분야가 바로 생성 모델이다. 이번 챕터에서는 베이지안 통계학의 기본 개념과 간단한 예제를 통해 베이지안 통계학이 어떻게 동작하는지 살펴보자.
Frequentist와 Bayesian
통계학을 배우는 목적은 여러 가지가 있는데, 그 중 하나는 확률분포를 결정하는 모수(unknown parameter)를 추정하는 것이다. 모수(unknown parameter)를 과학적으로 추정하려고 시도한 결과, 모수를 바라보는 여러 관점들이 나타났다. 그 중 두 가지가 바로 빈도론자(Frequentist)와 베이지안(Bayesian)이다. 대표적인 통계적 실험인 동전 던지기로 빈도론자와 베이지안의 차이를 이해해보자.
우리는 동전을 던져서 앞면이 나오는 횟수에 관심이 있다고 하자. 동전을 여러 번 던졌을 때 앞면이 나올 횟수는 동전을 한 번 던졌을 때 앞면이나 뒷면이 나올 확률에 영향을 받을 것이다. 즉, 한 번 던졌을 때 앞면이 나올 확률이 매우 높다면 여러 번 던졌을 때도 앞면이 많이 나올 것이고 그렇지 않으면 반대의 경우가 나타날 것이다. 앞면이 나올 확률을 θ라고 하면, N번 동전을 던졌을 때 앞면이 나올 횟수는 이항분포(N, θ)를 따르게 된다. 여기서 θ가 바로 분포를 결정하는 모수이다.
빈도론자들은 모수가 알려지지 않았으나 고정된 상수라고 생각한다. 동전에 이상이 없다면, 객관적으로 앞면과 뒷면이 나올 확률이 동일하므로 θ=0.5 처럼 특정 값으로 추정할 수 있다. 혹은 표본을 뽑아서 표본통계량들의 분포로부터 모수의 신뢰 구간을 추정하게 된다.
반면, 베이지안들은 모수가 어떤 확률분포를 따르는 확률변수라고 생각한다. 동전에 이상이 없다고 어떻게 확신할 수 있을까? 미세한 균열 같은 외부 변수가 영향을 줄 수도 있다. 그렇기에 베이지안은 θ를 처럼 어떤 분포를 따르는 확률변수로 정의하고, 실제 데이터가 주어졌을 때 θ의 조건부 분포를 구해서 추론하게 된다. 모수에 부여한 분포는 연구자의 주관이 들어가기 때문에, 확률을 확신의 정도로 해석할 수 있다.
왜 Bayesian을 딥 러닝에 사용하는가?
베이지안 통계학에서 연구해왔던 수치적인 적분 방법 및 함수 근사 방법들이 딥 러닝 계산에 쓰이며, 딥 러닝 모델의 하이퍼파라미터(Hperparameter)를 최적화할 때 쓰이기도 한다. 그리고 베이지안을 이용해서 딥 러닝의 예측 불확실성을 표현할 수 있으므로, 안전성이 중요한 자율주행, 의료, 금융 등의 영역에서 활발히 연구되고 있다.
확률분포 및 분포함수
데이터를 여러 번 수집하게 되면, 자주 나오는 값들이 있고 자주 나오지 않고 드물게 발생하는 값들이 있다. 데이터의 발생 가능성을 나타내는 정보가 확률 분포이다. 그리고 확률 분포를 간단하게 나타내기 위해 발생할 수 있는 각 사건들을 어떤 숫자로 변환하고, 각 숫자들에 대해서 확률을 부여하게 되면 어떤 사건이 많이 발생하는지 함수로 표현할 수 있다. 이 함수들을 확률 질량 함수 혹은 확률 밀도 함수라고 부른다. 동전을 3번 던지는 실험을 예로 들어보자.
실험을 통해 발생 가능한 경우들의 집합을 표본 공간이라고 한다. 이 실험의 표본 공간은 총 8개의 원소로 구성된다. 앞면이 한 번 혹은 두 번 나오는 경우가 더 많은 것을 알 수 있다.
$$ S = \left\{(T,T,T), (H,T,T), (T,H,T), (T,T,H), (H,H,T),(H,T,H),(T,H,H),(H,H,H) \right\} $$
표본 공간을 확률 변수를 이용해서 범주화 할 수 있다. 예를 들어, 확률변수 X를 앞면이 나올 횟수라고 정하게 되면, X는 0, 1, 2, 3의 값을 가지게 된다. 그리고 각 원소들은 다음과 같이 대응 된다.
| X | 0 | 1 | 2 | 3 |
| 원소 | (T,T,T) | (H,T,T), (T,H,T), (T,T,H) | (H,H,T), (H,T,H), (T,H,H) | (H,H,H) |
앞/뒷면이 발생할 가능성이 같다고 하면, 확률 분포는 다음과 같이 정해진다.
| X | 0 | 1 | 2 | 3 |
| 원소 | (T,T,T) | (H,T,T), (T,H,T), (T,T,H) | (H,H,T), (H,T,H), (T,H,H) | (H,H,H) |
| 확률 | 1/8 | 3/8 | 3/8 | 1/8 |
이를 수학적으로 표현하면, 다음과 같은 하나의 질량 함수로 일반화 할 수 있다.
$$ P(X=x) = P_{x}(x) = \binom{3}{x}0.5^{x}(1-0.5)^{3-x} $$
0.5를 모수 θ로 표현하면, 발생확률이 다른 이항 분포에도 위의 논리를 적용 가능하다.
Joint Distribution, Marginal Distribution
동일한 표본공간에서 정의되는 두 개 (이상)의 확률변수의 분포를 결합확률분포(joint distribution)이라고 하며, 결합확률분포를 이루는 각 변수의 확률분포를 주변확률분포(marginal distribution)라고 한다. 주변확률분포는 결합확률분포를 다른 변수들에 대해서 적분하면 얻을 수 있다. 확률변수가 연속형 일 때, 둘의 관계는 다음과 같다.
$$ f_{x}(x)\int_{-\infty }^{\infty }f_{x,y}(x,y)dy $$
조건부 분포(Conditional Distribution)
특정 확률변수의 값이 주어졌을 때, 다른 확률변수의 분포를 조건부 분포라고 한다. Y가 주어졌을 때, X의 조건부 분포는 다음과 같다.
$$ f_{x|y}(x|y) = \frac{f_{x,y}(x,y)}{f_{y}(y)} $$
위의 식에서 결합확률분포는 조건부 확률 분포와 주변 확률 분포의 곱임을 알 수 있다.
$$ f_{x|y}(x|y)f_{y}(y) = f_{x,y}(x,y) $$
Likelihood, Likelihood Function, Maximum Likelihood Estimation
최대 가능도 추정법은 미지의 모수 θ의 후보들 중에서, 밀도 함수를 이용해서 주어진 데이터들이 따를 가능성이 가장 높은 분포의 모수를 역으로 찾는 방법이다. 모수 θ가 주어졌을 때 확률분포 X에 대한 확률 밀도 함수는 다음처럼 주어진다. 여기서 밀도 함수는 모수 θ는 상수로 고정된, X의 함수이다.
$$ f_{x}(x) = f_{x}(x; \theta ) $$
반면, 데이터가 주어진 상황에서 모수를 역으로 찾는 상황에서는 밀도 함수를 X가 고정되고, 모수 θ의 함수로 바라보게 된다. 이 밀도 함수가 바로 가능도 함수이다. 가능도 함수랑 확률 밀도 함수는 동일한 함수이지만, X의 함수인지 θ의 함수인지가 다른 것이다.
$$ L(\theta ) = f_{x}(x;\theta) $$
따라서, 모수 θ의 최대 가능도 추정량 은 가능도 함수를 최대화하는 θ값이다.
$$ \hat{\theta } = argmax_{\theta }L(\theta) $$
Prior Distribution
베이지안 통계 연구자가 사전에 부여한, 모수 θ에 대한 확률 분포를 말한다. 확률 분포는 아래 처럼 표현할 수 있다.
$$ \pi _{\theta}(\theta) $$
Posterior Distribution
새로운 데이터 x가 주어졌을 때, 모수 θ의 조건부 확률 분포를 의미한다. 확률 분포는 아래 처럼 표현할 수 있다.
$$ f_{\theta|X}(\theta|x) $$
Posterior Distribution 구하기
Posterior Distribution을 구할 때 베이즈 정리를 이용하기 때문에, 이러한 접근법을 이용해서 모수를 추론하는 방법을 베이지안 추론(Bayesian Inference)이라고 부른다. 베이즈 정리는 다음과 같다.
$$ P(A|B) = \frac{P(A\cap B)}{P(B)} = \frac{P(B|A)P(A)}{P(B)} $$
Prior와 Likelihood를 베이즈 정리에 적용해서, Posterior Distribution을 구할 수 있다.
$$ f_{\theta|X}(\theta|x) = \frac{f_{\theta,x}(\theta,X)}{f_{x}(x)} = \frac{f_{x|\theta}(x|\theta)\pi _{\theta}(\theta)}{f_{x}(x)} $$
베이지안 통계에서는 모수도 확률 변수로 생각하기 때문에, Likelihood는 다음처럼 정의된다.
$$ L(\theta) = f_{X|\theta}(x|\theta) $$
베이지안 딥 러닝
일반적인 Neural Network는 학습하게 되면, 신경망의 Weight가 상수로 정해진다. 그렇기 때문에, 신경망은 사전에 학습하지 않은 데이터가 들어오더라도 무조건 하나의 값을 출력하게 된다. 하지만, 사전에 학습하지 않은 데이터라면 다양한 예측이 가능하다고 알려주는 게 더 낫다. 예측 결과를 보고, 연구자가 데이터를 더 추가할 지 결정해서 성능을 더 향상시킬 수 있기 때문이다.
신경망의 Weight가 고정된 값이 아니라 어떤 분포가 된다면, 이처럼 예측 평균과 분산을 이용해서 예측 범위를 나타낼 수 있다. Weight가 분포가 되는 신경망을 베이지안 신경망이라고 하며, Weight는 Posterior Distribution이 된다. 예측할 때는, Posterior Distribution에서 샘플링 한 값을 이용하게 된다.

문제는 Posterior Distribution을 구하는 것이 일반적으로 불가능하기 때문에, Weight W에 대해서 모수 θ를 가지는 임의의 Variational Distribution를 가정한 다음 이를 Posterior Distribution으로 근사시킨 다음 Variational Distribution를 사용하게 된다. 이를 Variational Inference라고 한다. Variational Distribution은 아래와 같다.
$$ q_{\theta}(W) $$

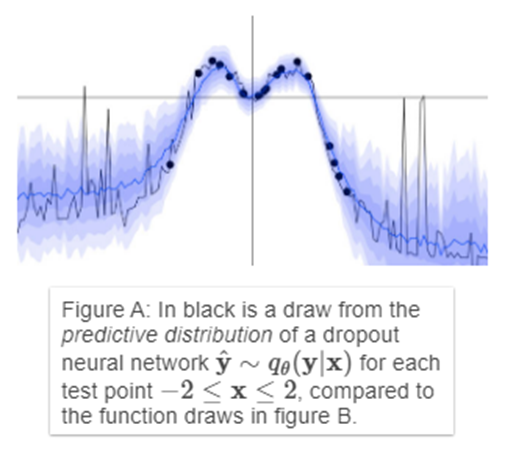
이렇게 베이지안 신경망을 학습시키면, 불확실성을 모델링 할 수 있다. 아래의 그래프를 보면, 데이터를 학습한 구간에서는 신뢰 구간이 좁게 나타나고 학습하지 않은 부분에서는 신뢰 구간이 점점 넓어지는 것을 볼 수 있다.
글 | 전 AI1팀 권기범
옮김 | AI기술연구2팀 김찬경

'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 4-4. Seq2Seq (0) | 2023.11.30 |
|---|---|
| Chapter 4-3. RNN (0) | 2023.10.26 |
| Chapter 4. 신경망과 딥러닝 (0) | 2023.08.31 |
| Chapter 3-8. 비지도 학습 (0) | 2023.07.26 |
| Chapter 3-7. GAM 이론 및 실습 (0) | 2023.06.29 |





댓글