Chapter 3-8. 비지도 학습
대부분의 흔히 알고있는 머신러닝 알고리즘은 지도 학습 기반의 알고리즘입니다. 이는 이전 챕터들에서도 소개되었지만, 데이터에 정답(레이블)이 알고 있는 상태로 학습을 하는 방식입니다. 본 챕터에서는 지도 학습과 상반되는 비지도 학습이 무엇이며, 왜 필요한지 그리고 어떤 문제에 적용하여 사용할 수 있는지에 대해 알아보겠습니다.
현실 세계에서 우리가 다룰수 있는 대부분의 데이터들은 정답(레이블)이 없는 데이터입니다. 그렇다면 어떻게 대부분의 지도 학습에 적용될 수 있었을까요?
이는 사람이 직접 데이터에서 라벨링 처리 과정을 수행했기 때문입니다. 이는 굉장히 비효율적이고 사람이 직접 수행하다보니 실수도 발생할 수 있고 또 많은 비용들이 발생하게 됩니다.
그렇기때문에 라벨링 처리가 없어도 데이터의 특성이나 패턴을 학습하는 비지도 학습이 등장했습니다.
이전 챕터들에서 다뤘던 차원 축소의 주성분분석이 비지도 학습의 대표적인 알고리즘이라고 할 수 있겠습니다. (정답 데이터 없이 스스로 학습을 통해 주성분의 축을 결정함)
비지도 학습 방식은 오로지 주어진 데이터 안에서 특정한 패턴이나 규칙을 찾습니다. 온전히 데이터를 기반으로 결과를 유추하기 때문에 입력 데이터에 대해 상당히 의존적인 특성이 있습니다. 또한 지도 학습과 달리 정답 데이터가 없기때문에 결과에 대한 성능 평가가 다소 어려운 편입니다. 이러한 비지도 학습의 대표적인 알고리즘에는 차원 축소, 이상치 탐지, 군집과 같은 개념들이 있습니다.
군집 (Clustering)
데이터셋에서 비슷한 데이터끼리 일정 개수의 샘플로 그룹을 만드는 작업을 군집화라고 말합니다. 분류 (Classification) 와 비슷하게 동작하지만, 군집은 엄연한 비지도 학습의 일종입니다.
입력 데이터들은 데이터의 특성을 고려하여 그룹을 생성하고 같은 그룹, 즉 군집에 속하는 데이터들은 비슷한 성질 (위치, 평균, 편차 등)을 갖습니다. 군집이 적용될 수 있는 문제의 예시로는 고객 분류를 통한 추천시스템, 차원 축소, 이상 데이터 탐지, 이미지 분할 등 다양한 목적으로 사용될 수 있습니다.
대표적인 군집화 알고리즘인 K-Means , DBSCAN , HCA 그리고 GMM 대해 알아보겠습니다.
K-Means
K-Means 군집화는 데이터셋에서 임의의 중심점인 Centroid 를 찾아, 그 점을 기준으로 하여 최소 거리에 기반한 군집화를 진행합니다. K-Means 에서 'K' 의 의미는 몇 개의 군집으로 데이터를 그룹화할 지 예상하는 군집의 개수를 뜻합니다. 예를 들어 'K=5' 라면 해당 알고리즘은 입력 데이터셋을 총 5 개의 군집으로 나누고자 할 것입니다. 'Means' 는 각 군집에서 중심점 (Centroid)과 각 데이터들의 평균 거리값을 의미합니다.
[알고리즘 작동 방식]
1) 무작위 K 개의 샘플을 뽑아 Centroid 설정
2) 각 군집에 데이터 샘플 할당 및 Centroid 업데이트 (해당 군집에서의 중심점으로 이동)
3) Centroid 에 더 이상 변화가 없을 때까지 반복
이전 챕터에서 다루었던 'iris 데이터셋' 을 통해 간단한 K-Means 예제를 살펴보겠습니다.
In[1]:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# iris 예제 데이터 로드
iris = sns.load_dataset('iris')
iris.head()Out[1]:
sepal_length sepal_width petal_length petal_width species
0 5.1 3.5 1.4 0.2 setosa
1 4.9 3.0 1.4 0.2 setosa
2 4.7 3.2 1.3 0.2 setosa
3 4.6 3.1 1.5 0.2 setosa
4 5.0 3.6 1.4 0.2 setosa
In[2]:
# iris (petal) 데이터 분포 시각화
plt.figure(figsize=(18,10))
plt.scatter(iris['petal_length'], iris['petal_width'])
plt.title("iris-petal", fontsize=20)
plt.xlabel("length")
plt.ylabel("width")Out[2]:

iris 데이터에는 꽃의 종류인 'setosa', 'versicolor', 'virginica' 3가지 꽃에 대해 레이블이 되어있는 것을 이미 알고 있습니다. (Out[1])
하지만 petal (꽃잎)에 대한 length, width 데이터만을 사용하여 레이블이 없는 데이터라고 가정하고 K-Means 군집화를 진행하겠습니다.
Out[2] 에서 petal (꽃잎) 에 대한 데이터만을 가지고 데이터의 분포를 해석하자면, 왼쪽 아래에 뭉쳐있는 데이터 집단과 우상단에 뭉쳐있는 나머지 데이터 집단, 총 2가지 군집으로 분리하는 것을 기대할 수 있겠습니다.
In[3]:
from sklearn.cluster import KMeans
k = 2
X = iris[['petal_length']]
y = iris[['petal_width']]
model = KMeans(n_clusters=k)
iris['cluster'] = model.fit_predict(X,y)
irisOut[3]:
sepal_length sepal_width petal_length petal_width species cluster
0 5.1 3.5 1.4 0.2 setosa 1
1 4.9 3.0 1.4 0.2 setosa 1
2 4.7 3.2 1.3 0.2 setosa 1
3 4.6 3.1 1.5 0.2 setosa 1
4 5.0 3.6 1.4 0.2 setosa 1
In[4]:
# iris (petal) 군집 결과 시각화
plt.figure(figsize=(8,8))
for i in range(k):
plt.scatter(
iris.loc[iris['cluster']==i, 'petal_length'],
iris.loc[iris['cluster']==i, 'petal_width'],
label='cluster'+str(i)
)
plt.title(f"K={k}", fontsize=20)
plt.xlabel("length")
plt.ylabel("width")
plt.legend()
plt.show()Out[4]:

위 시각화 이미지는 군집의 개수 k = 2, 3, 4, 5 까지의 결과에 대한 각 시각화 결과입니다. 그렇다면 어떻게 적절한 군집의 개수 k 를 결정할 수 있을까요?
저의 주관적인 관점으로는 k 의 개수는 2 일 때, 군집화가 적절하게 이루어졌다고 판단할 것 같아보입니다.
다음은 객관적인 최적의 k 개수를 구하는데는 사용되는 실루엣 점수 (Silhouette Score) 를 통해 적절한 k 의 개수를 추정해보겠습니다.
실루엣
실루엣이란, 각 군집간의 거리가 얼마나 잘 분리 돼있는지 계산을 통해 나타낸 수치입니다.
$$s(i) = \frac{(b(i)-a(i))}{(max(a(i),b(i)))}$$
[실루엣 점수 (S)]
a : 클러스터 내부의 평균 거리
b : 가장 가까운 다른 클러스터의 샘플까지의 거리
실루엣 점수의 범위는 -1 ~ 1 사이의 값을 가지며, 1에 가까울수록 (a) 클러스터 내부안에 샘플들이 잘 속해 있고, (b) 다른 클러스터와는 멀리 떨어져 있어, 적절히 군집화 되었다고 해석할 수 있습니다.
Python sklearn 모듈에도 이와 같은 실루엣 계산을 해주는 메소드를 지원하고 있습니다. 실루엣 점수는 클러스터링(비지도 학습)의 성능 평가 지표로써 사용될 수 있겠습니다.
In[5]:
from sklearn.metrics import silhouette_samples, silhouette_score
# iris (petal) 실루엣 계수 값
score_samples = silhouette_samples(iris[['petal_length','petal_width']], iris['cluster'])
iris['silhouette_coef'] = score_samples
print(f'silhouette_samples:{score_samples.shape}')
# 실루엣 점수
average_score = silhouette_score(iris[['petal_length','petal_width']], iris['cluster'])
print(f'iris silhouette_score:{average_score}')
iris.groupby('cluster')['silhouette_coef'].mean()Out[5]:
silhouette_samples:(150,)
iris silhouette_score:0.7653904101258123
cluster
0 0.690246
1 0.911260
Name: silhouette_coef, dtype: float64[k = 2 일때 실루엣 점수]
- 전체 데이터의 평균 점수는 0.76
- "0번 클러스터"는 평균보다 이하
- "1번 클러스터"는 더 좋은 값
silhouette_samples:(150,)
iris silhouette_score:0.6549487761651254
cluster
0 0.919582
1 0.552856
2 0.487152
Name: silhouette_coef, dtype: float64[k = 3 일때 실루엣 점수]
- 전체 데이터의 평균 점수는 0.65
- "0번 클러스터"는 더 좋은 값
- "1번, 2번 클러스터" 모두 평균 이하 값
실루엣 점수를 기반으로 클러스터의 개수를 판단한다면 k = 2 일 때와 k = 3 일 때 비슷한 결과를 나타낼 것 같습니다.
군집화 이전에 데이터의 분포만을 가지고 추정했을 때에 비해 3가지로 군집해도 괜찮을 수 있다는 인사이트를 얻을 수 있습니다.
K-Means 알고리즘은 빠른 학습속도와 넓은 확장성을 가졌지만, 결국 Centroid 중심값이 초기에 무작위로 선택되어 초기값에 민감하고, 군집 내에 분산 구조를 반영하지 못한다는 한계점이 존재합니다.
HCA (계층적 군집 분석)
HCA 는 비슷한 군집끼리 묶고, 각 그룹을 더 작은 그룹으로 세분화하여 최종적으로는 하나의 데이터 집단으로만 구성될 때까지 클러스터링을 계층적으로 수행하는 알고리즘 입니다.
동작 방식은 군집 간의 거리를 기반으로 클러스터링이 수행되며, K-Means 와 다르게 클러스터의 개수를 사전에 정하지 않아도 됩니다. Python Sklearn 에서는 'dendrogram' 을 통해 구현합니다.
In[6]:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.cluster.hierarchy import linkage, dendrogram
iris = sns.load_dataset('iris')
# 문자 -> 벡터 치환
for i in range(len(iris)):
if iris.loc[i, "species"] == 'setosa':
iris.loc[i, "species"] = 0
elif iris.loc[i, "species"] == 'versicolor':
iris.loc[i, "species"] = 1
elif iris.loc[i, "species"] == 'virginica':
iris.loc[i, "species"] = 2
mergings = linkage(iris, method="complete")
plt.figure(figsize=(40,20))
dendrogram(mergings, leaf_rotation=90, leaf_font_size=20)
plt.show()Out[6]:

iris 데이터셋에 대한 HCA 계층 분석 결과입니다. 덴드로그램을 통해 데이터들의 유사성을 기준으로 한 군집화 결과를 확인할 수 있습니다. 계층 분석에서 군집의 개수를 정할 때는 덴드로그램의 y 축 위치를 기준으로 정합니다.
y 축 위치를 높게 잡는다면 적은 군집의 수와 유사성 수준은 낮게 구성될 것이고,
y 축 위치를 낮게 잡는다면 유사성 수준은 높아지겠지만 군집의 개수는 많아질 것 입니다.
DBSCAN (Density-Based Spatial Clustering of Applications with Noise)
DBSCAN이란 클러스터링 알고리즘 중 밀도를 기반으로 하는 군집을 수행하는 알고리즘입니다. 앞서 설명한 K-Means, HCA 는 데이터들간의 거리를 기반으로 군집을 결정짓는 방식이지만, DBSCAN의 아이디어는 데이터들의 밀집도가 높은 구역을 기준으로 군집을 결정하는 방식입니다.
밀도 기반의 군집의 가장 큰 특징은 두 데이터의 거리가 멀더라도 같은 군집에 속할 수 있다는 점입니다. 이는 두 데이터를 연결해주는 또 다른 데이터들이 밀도있게 위치한다면 같은 군집이 될 수 있습니다.

아주 작은 거리 단위인 ε (입실론) 을 기준으로 반경 내에 데이터 샘플이 n 개 이상 있다면, 해당 클러스터를 형성하는 방식으로 동작합니다. 거리 기반이 아닌 데이터 밀도를 기반으로하여 군집을 만들어내기에 군집의 기하학적인 모양에서도 좋은 성능을 보입니다. 주로 데이터 밀도(클러스터)에 포함되지 못하는 Noise point 검출에 활용될 수 있습니다.
K-Means 에서 처럼 사전에 클러스터의 개수를 설정하진 않지만, 입실론 반경에 대한 파라미터 값의 설정이 필요합니다. (default = 0.5)
In[7]:
from sklearn.cluster import DBSCAN
model = DBSCAN(eps=0.3, min_samples=5)
iris['cluster'] = model.fit_predict(iris[['petal_length']], iris[['petal_width']])
n = len(iris['cluster'].unique())
plt.figure(figsize=(8,8))
for i in range(n):
plt.scatter(
iris.loc[iris['cluster']==i, 'petal_length'],
iris.loc[iris['cluster']==i, 'petal_width'],
label='cluster'+str(i)
)
plt.title("eplison=0.3", fontsize=20)
plt.xlabel("length")
plt.ylabel("width")
plt.show()Out[7]:

지금까지 소개한 군집 알고리즘들 이외에도 Python Sklearn 패키지에는 병합 군집, BIRCH, 평균-이동, 유사도 전파 등의 다양한 군집 알고리즘들을 지원합니다. 사용하고자하는 각 데이터에 대한 이해를 기반으로 목적에 맞는 알고리즘을 적절히 선택하고 사용하는 것이 중요하겠습니다.
가우시안 혼합 모델 (Gaussian Mixture Model)
GMM 에 대해 설명하기 앞서 '가우시안' 이란 용어에 대해 다시 한번 정리하겠습니다. 가우시안 분포는 통계에서 말하는 정규 분포와 동일한 분포를 말합니다. 수학자들은 정규 분포라고 말하고, 공학자들은 가우시안 분포라고 말하는 경향이 있다고 합니다. 앞으로 이야기할 가우시안 분포와 정규 분포는 같은 분포를 의미하는 것입니다.
정규 분포란, 평균에 가까울수록 발생 확률이 증가하고 멀어질수록 발생 확률이 줄어듭니다. 즉 대부분의 데이터는 평균의 근처에서 많이 발생한다고 생각할 수 있습니다. 정규 분포 함수는 평균을 중심으로 분산 값만큼 좌우대칭의 종 모양의 분포를 나타냅니다.

가우시안 혼합 모델이란, 이름 그대로 가우시안 분포 여러 개가 혼합된 클러스터링 모델을 말합니다. 혼합 모델이라함은 통계학에서 전체 집단 속에 하위 집단의 존재를 나타내는 확률을 의미합니다. 즉 관찰된 데이터의 전체 분포는 일부 특성들로 구성되는 몇 개의 하위 집단으로 혼합되어있음을 가정하고, 특정 하위 분포에 속할 확률을 추론하고자 합니다.

알고리즘 이름에서 'Mixture Model' 앞의 'Gaussian' 붙은 의미는 하위 집단들이 정규 분포의 형태로 구성되어있음을 가정하는 것입니다. 하위 정규 분포에 속하는 데이터들을 하나의 그룹으로 묶어 군집화하는 아이디어인 셈입니다. 그렇다면 앞에서 이야기하던 K-Means 와 차이점은 무엇일까요?
K-Means 의 한계점으로도 이야기했지만, K-Means 알고리즘의 경우 그룹 내 데이터들의 분산을 고려하지 않습니다. 하지만 GMM 에서는 가중치, 평균, 공분산을 이용하여 클러스터를 추정하기 때문에 그룹 내 데이터들의 분산이 고려됩니다.
또한 그러한 이유로 K-Means 의 경우 타원형 데이터 분포에 취약하지만 (성능이 좋지않음) , GMM 에서는 타원형 데이터 분포도 잘 반영할 수 있습니다. 그림을 보며 자세히 설명해보겠습니다.

그림에서 3개의 가우시안 분포로 구성된 데이터셋 Info
| 포함되는 샘플의 수 | 평균 값 | 표준편차 값 | |
| 가우시안 분포 (파란색) | 2,000 | -0.5 | 0.2 |
| 가우시안 분포 (보라색) | 5,000 | -0.1 | 0.07 |
| 가우시안 분포 (검정색) | 10,000 | 0.2 | 0.13 |
위 그림에서 하위 가우시안에 대한 정보를 모르는 상태로 해당 데이터셋을 만났다면 다음과 같은 상황일 것 이다.

GMM 을 통한 모수 추정은 다음과 같다 (Python Sklearn 패키지 GaussianMixture 계산 생략)
| 실제 모수 | GMM 추정한 모수 | |
| Weight 1 | 2000/(2000+5000+10000) = 0.117 |
0.101 |
| Weight 2 | 0.294 | 0.391 |
| Weight 3 | 0.588 | 0.509 |
| 평균 1 | -0.5 | -0.54 |
| 평균 2 | -0.1 | -0.07 |
| 평균 3 | 0.2 | 0.227 |
| 표준편차 1 | 0.2 | 0.168 |
| 표준편차 2 | 0.07 | 0.094 |
| 표준편차 3 | 0.13 | 0.113 |
GMM 이 무엇을 추정하는지 어느정도 이해했다면, 이를 iris 데이터셋을 통해 검증해보겠습니다.
In[8]:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
iris = sns.load_dataset('iris')
plt.figure(figsize=(10,8))
plt.scatter(iris['petal_length'], iris['petal_width'], color='black', linewidths=0)
plt.xlabel('length')
plt.ylabel('width')
plt.show()
Out[8]:

In[9]:
from sklearn.mixture import GaussianMixture
petal = iris[['petal_length','petal_width']]
gmm_comp_2 = GaussianMixture(n_components=2, n_init=10)
gmm_comp_3 = GaussianMixture(n_components=3, n_init=10)
gmm_comp_2.fit(petal)
gmm_comp_3.fit(petal)
iris['gmm_comp_2_label'] = gmm_comp_2.predict(petal)
iris['gmm_comp_3_label'] = gmm_comp_3.predict(petal)
iris.groupby(['species'])['gmm_comp_2_label'].value_counts()
iris.groupby(['species'])['gmm_comp_3_label'].value_counts()Out[9]:
species gmm_comp_2_label
setosa 0 50
versicolor 1 50
virginica 1 50
Name: count, dtype: int64
species gmm_comp_3_label
setosa 1 50
versicolor 0 49
2 1
virginica 2 47
0 3
Name: count, dtype: int64실제 정답(레이블)과 클러스터_2 와 클러스터_3 에서 군집화 결과를 각각 비교 해석해보겠습니다.
클러스터_2 에서는 50개씩 온전하게 분류하였으며, 클러스터_3 에서는 전체 150개의 데이터 중 versicolor 에서 1개, virginica 에서 3개를 잘못 분류했지만, 3개의 군집 분류도 적용할 수 있다는 인사이트를 찾아낼 수가 있습니다.
In[10]:
plt.figure(figsize=(10,8))
for i in range(2):
plt.scatter(
iris.loc[iris['gmm_comp_2_label']==i, 'petal_length'],
iris.loc[iris['gmm_comp_2_label']==i, 'petal_width'],
label='cluster'+str(i)
)
plt.xlabel("length")
plt.ylabel("width")
plt.show()Out[10]:

다음으로는 GMM 에서의 군집의 개수(n_components)를 최적화하는 방법을 설명하겠습니다.
정보이론에서 사용되는 BIC(Bayesian information criterion), AIC(Akaike information criterion)의 개념을 사용합니다.
즉 ‘Information criterion’ 을 최소화하는 지점을 찾아 군집의 개수를 최적화할 수 있습니다.
In[11]:
bic = [450,450]
aic = [450,450]
for i in range(2,7): # 군집 개수만큼
gmm = GaussianMixture(n_components=i).fit(petal)
if gmm:
bic.append(gmm.bic(petal))
aic.append(gmm.aic(petal))
plt.figure(figsize=(10,4))
plt.plot(bic, '-d', label='bic')
plt.plot(aic, '--d', color='red', label='aic')
plt.xlabel("n_comps")
plt.ylabel("information criterion")
plt.legend()
plt.show()Out[11]:
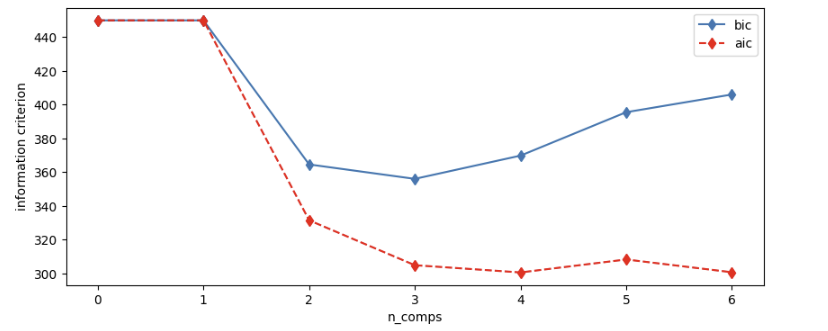
다음 AIC 와 BIC 값을 통해 적절한 군집의 수는 함께 감소하며 최저인 지점인 n_comps = 3 일 때 좋은 선택으로 보입니다.
혼합 모델 개념에서 더 나아가, 최적의 클러스터 개수를 직접 분석하지 않고, 불필요한 클러스터의 가중치를 0 으로 만들어주는 Bayesian-GMM (BGM) 이라는 것도 존재합니다.
In[12]:
import numpy as np
from sklearn.mixture import BayesianGaussianMixture
bgm = BayesianGaussianMixture(n_components=10, n_init=10)
bgm.fit(petal)
np.round(bgm.weights_, 2)Out[12]:
array([0.34, 0.31, 0.35, 0. , 0. , 0. , 0. , 0. , 0. , 0. ])
BGM 에서는 n_components 는 기대하는 최적의 클러스터보다 충분히 넉넉한 값을 입력해줍니다. (n_components=10)
결과를 통해 3번째 클러스터까지 가중치가 부여된 것을 확인할 수 있습니다. 이 외에도 다양한 변종 GMM 모델들이 존재합니다.
* 이미지 출처:
https://3months.tistory.com/154
기획 및 글 | AI기술연구팀 유용빈

'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 4-2. 기초 베이지안 통계 (0) | 2023.09.21 |
|---|---|
| Chapter 4. 신경망과 딥러닝 (0) | 2023.08.31 |
| Chapter 3-7. GAM 이론 및 실습 (0) | 2023.06.29 |
| Chapter 3-6. 차원 축소 (0) | 2023.05.25 |
| Chapter 3-5. 서포트 벡터 머신 (Support Vector Machine) (0) | 2023.04.27 |





댓글