Chapter 3-7. GAM 이론 및 실습
일반적인 선형 회귀분석은 모형의 단순성으로 인해 해석과 추론이 쉽다는 장점이 있으나 예측력이라는 중요한 부분에서 한계를 가진다. 선형모형은 회귀 문제에서 독립변수와 예측변수가 선형적 관계가 있다고 가정한다. 이러한 가정이 맞는 경우도 있지만 부정확한 경우도 얼마든지 존재한다. 일반화 가법 모형(Generalized Additive Model)은 선형 가정을 완화시키는 가장 강력한 추론 방법이다.
일반화 가법 모형과 선형회귀 모형의 차이를 간단한 예제를 통해 설명하겠다.
R MASS 패키지에 포함되어 있는 mcycle 데이터는 모터사이클 사고 모의실험을 통해 머리의 가속과 감속을 측정한 자료이다. 해당 데이터에서 times 필드는 충돌 후 시간(millsecond)이고 accel 필드는 속도가 단위시간 동안 얼마나 크게 변화하는가를 나타내는 벡터양으로 단위는 m/sec2 이다.
데이터를 로드 후 프린트하면 다음과 같다.
In[1]:
import pandas as pd
mycle = pd.read_csv("./mycle.csv", index_col=0)
mycleOut[1]:

시간과 가속도의 관계를 plotly-express 라이브러리를 이용하여 산점도로 표현하면 다음과 같다.
In[2]:
import plotly.express as px
import plotly.graph_objects as go
fig = px.scatter(mycle, x="time", y="accel")
fig.show()Out[2]:

해당 데이터를 독립 변수(X)를 시간, 예측 변수(Y)를 가속도로 하는 선형회귀 모형에 적합한 결과 아래와 같은 그래프를 볼 수 있다. 선형회귀 모형을 학습하기 위하여 파이썬 rpy2 라이브러리 및 R의 lm 함수를 활용하였다.
In[3]:
import numpy as np
import rpy2.robjects as ro
from rpy2.robjects.packages import importr
from rpy2.robjects import pandas2ri
from rpy2.robjects.conversion import localconverter
with localconverter(ro.default_converter + pandas2ri.converter):
R_mycle = ro.conversion.py2rpy(mycle)
lm_model = ro.r.lm(ro.Formula("accel ~ time"), data=R_mcycle)
mcycle["lm_fitted_value"] = np.array(lm_model.rx("fitted.values"))[0]
fig = px.scatter(mcycle, x="times", y="accel")
fig.add_trace(go.Scatter(x=mcycle["times"], y=mcycle["lm_fitted_value"], name="lm))
fig.show()Out[3]:
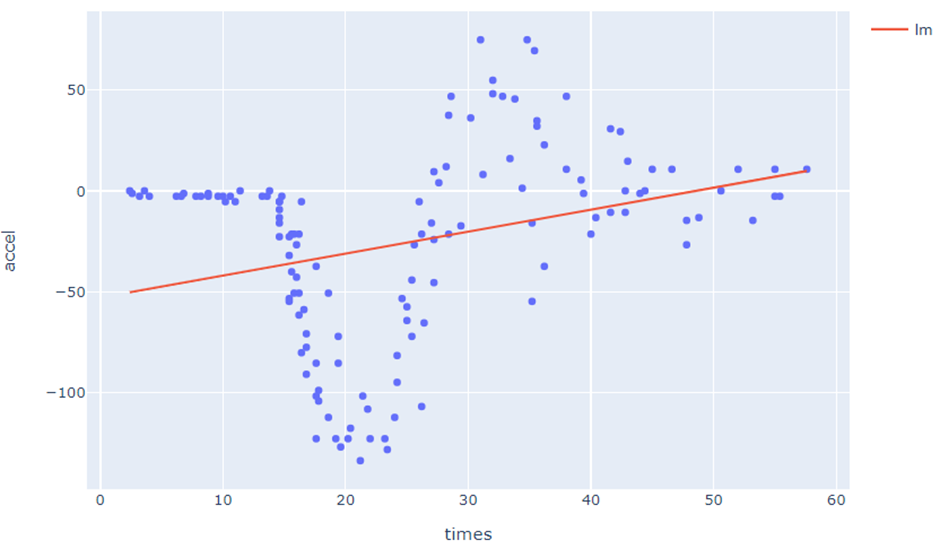
모형의 요약통계량을 summary 함수를 이용하여 확인하면 아래와 같다.
In[4]:
print(ro.r.summary(lm_model))Out[4]:

Adjusted R-squared값이 0.08로 상당히 작으며 그래프상으로 한눈에 봐도 설명력이 낮은 모형인 것을 알 수 있다.
일반화 가법 모형은 독립 변수와 예측 변수의 선형적 가정을 기반으로 하는 선형회귀 모형의 단점을 보완할 수 있다. R mgcv 패키지를 이용하여 간단하게 일반화 가법 모형을 구현할 수 있다. mgcv에서 제공하는 gam 함수를 사용하고 인자로는 formula(Y ~ X)와 data(분석 대상이 되는 데이터 셋)을 설정하여 실행한다.
In[5]:
importr('mgcv')
with localconverter(ro.default_converter + pandas2ri.converter):
R_mcycle = ro.conversion.py2rpy(mcycle)
gam_model = ro.r.gam(ro.Formula("accel ~ s(times)"), data=R_mcycle)
mcycle["gam_fitted_value"] = np.array(gam_model.rx("fitted.values"))[0]
fig = px.scatter(mcycle, x="times", y="accel")
fig.add_trace(go.Scatter(x=mcycle["times"], y=mcycle["gam_fitted_value"], name="gam"))
fig.show()Out[5]:

코드 상의 s(times)처럼 독립 변수를 smooth term으로 표현한다. Smooth term은 cubic spline interpolation 기법을 이용한 것을 의미한다. Cubic spline interpolation에 관해서는 아래에서 자세히 설명하겠다.
R summary 함수를 이용하여 gam 모델에 대한 요약 통계량을 확인하면 다음과 같다.
In[6]:
print(ro.r.summary(gam_model))Out[6]:

선형회귀 모형과 비교하여 Adjusted R-squared의 값이 0.78로 설명력이 크게 증가한 것을 볼 수 있다. GAM에서 사용한 비선형 적합은 cubic spline interpolation를 사용한 것이다. cubic spline interpolation은 각 구간 사이를 3차 방정식으로 추정하고 그 사이의 값을 추정하는 방법이다.
임의의 데이터 포인트 3개가 있다고 가정하자. x1의 좌표를 (1,2), x2의 좌표를 (2,3) x3의 좌표를 (3,5)라고 할 때 그래프는 아래와 같다.

여기서 각 점을 linear interpolation 한다고 가정하면 그래프는 아래와 같을 것이다.
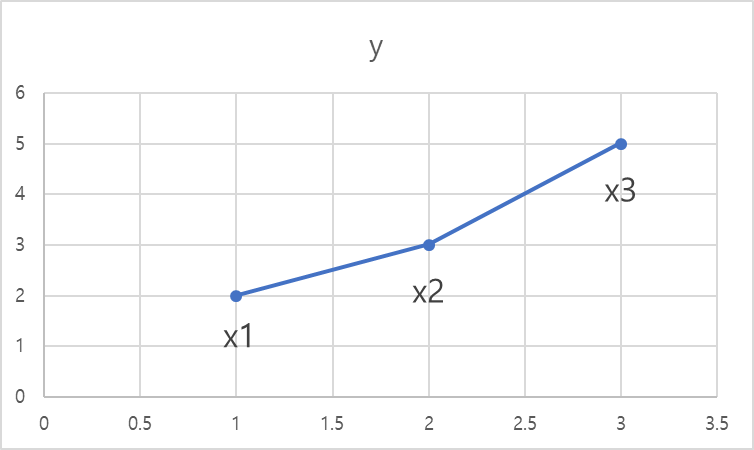
같은 데이터를 cubic spline interpolation 하면 아래 그래프와 같다.
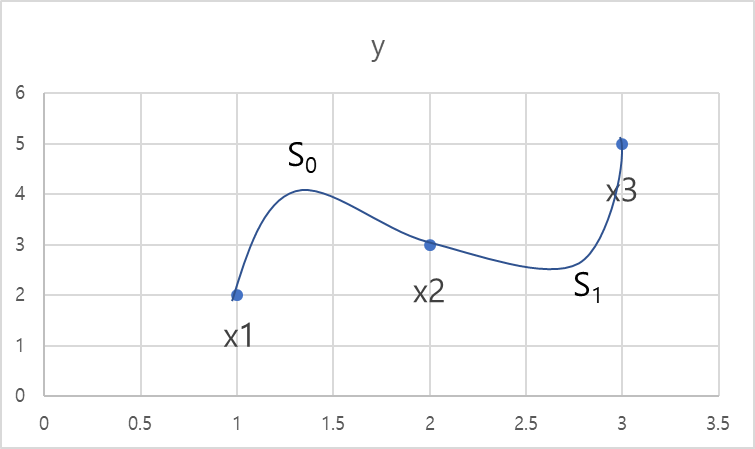
위 이미지처럼 x1, x2, x3의 점을 cubic spline interpolation 한다고 할 때 S0과, S1를 아래와 같은 스플라인 회귀식으로 추정할 수 있다.
$$ S_0(X) = a_0 + b_0(X-X_i) + c_0(X-X_i)^2 + d_0(X-X_i) ^3$$
$$S_1(X) = a_1 + b_1(X-X_i) + c_1(X-X_i)^2 + d_1(X-X_i)^3$$
미지수는 총 a0, b0, …, c1, d1까지 8개를 구해야 한다. 이처럼 점이 3개일 때 미지수의 총개수는 8개 (4*(3-1) = 8)이다.
8개의 미지수를 구하기 위해 아래의 조건을 활용한다.
1. 각 회귀식은 점을 지난다.
2. 각 회귀식 S0(X), S1(X)가 동시에 지나는 점에서의 값은 같다.
3. 동시에 지나는 점에서의 1차 도함수는 같다.
4. 동시에 지나는 점에서의 2차 도함수는 같다.
5. 각 회귀식의 1차 도함수는 원점을 지난다.
1번 조건을 적용하여 스플라인 회귀식을 아래처럼 표현할 수 있다.
$$S_0(X) = a_0 + b_0(x-1) + c_0(x-1)^2 + d_0(x-1)^3$$
$$S_1(X) = a_1 + b_1(x-2) + c_1(x-2)^2 + d_1(x-2)^3$$
각 회귀식은 점을 지난다는 조건으로 해당 회귀식을 계산하면 아래와 같다.
$$S_0(1) = 2, a_0 = 2$$
$$S_1(2) = 3, a_1 = 3$$
$$S_0(2) = 3, 2 + b_0 + C_0 + d_0 = 3 \rightarrow b_0 + c_0 + d_0 = 1 ----- (1)$$ $$S_1(3) = 5, 3+ b_1 + C_1 + d_1 = 5 \rightarrow b_1 + c_1 + d_1 = 2 ----- (2)$$
3, 4번 조건을 활용하기 위해 S0(X), S1(X)를 각각 1, 2차 미분하면 다음과 같다.
$$S_0'(X) = b_0 + 2c_0(x-1) +3d_0(x-1)^2, S_0''(X) = 2C_0 + 6d_0(x-1)$$
$$S_1'(X) = b_1 + 2c_1(x-2) + 3d_1(x-2)^2, S_1''(X) = 2c_1 + 6d_1(x-2)$$
$$S_0'(2) = S_1'(2)$$
$$b_0 + 2c_0 + 3d_0 = b_1 \rightarrow b_0 + 2c_0 + 3d_0 - b_1 = 0 ----- (3)$$ $$ S_0''(2) = S_1''(2)$$
$$2c_0 + 6d_0 = 2c_1 \to 2c_0 + 6d_0 - 2c_1 = 0 ----- (4)$$
5번 조건을 활용하여
$$S_0''(1) = 0, S_1''(3) = 0$$
$$S_0''(1) = 2C_0 = 0 \rightarrow C_0 = 0$$
$$S_1''(3) = 2c_1 + 6d_1 = 0 \to c_1 + 3d_1 = 0 ----- (5)$$
5가지 방정식을 활용하여 가우스 소거법으로 나머지 해를 구한다.
$$ \begin{pmatrix} 1 \quad1 \quad0 \quad0 \quad0 \\ 0 \quad0 \quad1 \quad1 \quad1 \\ 1 \quad3 -1 \quad0 \quad0 \\ 0 \quad3 \quad0 -1 \quad0 \\ 0 \quad0 \quad0 \quad1 \quad3 \\ \end{pmatrix}\begin{pmatrix} b_0 \\ d_0 \\ b_1 \\ c_1 \\ d_1 \\ \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 0 \\ 0 \\ 0 \\ \end{pmatrix}$$
가우스 소거법을 통해 5개의 미지수의 해를 구하면 다음과 같다.
$$b_0 = \frac{3}{4}, d_0 = \frac{1}{4}, b_1 = \frac{3}{2}, c_1 = \frac{3}{4}, d_1 = -\frac{1}{4}$$
이를 통해 회귀식을 완성하면 아래와 같다.
$$S_0(X) = 2 + \frac{3}{4}(x-1) + \frac{1}{4}(x-1)^3$$ $$S_1(X) = 3 + \frac{3}{2}(x-2) + \frac{4}{3}(x-2)^2 -\frac{1}{4}(x-2)^3$$
같은 X축에 점이 한 개가 아니라 여러 개일 경우 가우스 소거법으로 미지수를 구할 수 없다. 이 경우는 선형회귀 학습과 마찬가지로 최소제곱법을 통해 최적의 해를 구하게 된다. loss 함수를 수식으로 나타내면 아래와 같다.
$$loss = \sum_{i=1}^{n}(y_i-f(x_i))^2 + \lambda \int f''(t)2dt$$ $$\sum_{i=1}^{n}(y_i - f(x_i))^2$$
위 항은 f(x)의 예측값과 실제값의 오차를 줄이도록 학습하는 loss함수이며 λf''(t)2dt 항은 2차 미분 값으로 t에서의 기울기의 변화를 의미한다. 즉 함수가 얼마나 급격하게 변하는지에 대한 정보를 담고 있다. 여기서 함수가 급격하게 변한다는 것은 학습 데이터에 과적합(overfitting)된 것을 의미한다. 따라서 학습 데이터에 모두 반응하는 것이 아니라 smooth한 일반적인 모델을 만드는 것이 목적이다.
이처럼 Spline 곡선은 인접한 두 점 사이의 구간마다 별도의 다항식을 이용해 정의한 곡선이다. 다시 말해 전체 데이터를 하나의 다항식이 아닌 구간별 다항식으로 표현한 것이다. 일반화 가법 모형은 spline interpolation을 기반으로 데이터를 가장 잘 설명하는 최적의 비선형 적합을 할 수 있다.
글 | AI기술연구2팀 김찬경

'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 4. 신경망과 딥러닝 (0) | 2023.08.31 |
|---|---|
| Chapter 3-8. 비지도 학습 (0) | 2023.07.26 |
| Chapter 3-6. 차원 축소 (0) | 2023.05.25 |
| Chapter 3-5. 서포트 벡터 머신 (Support Vector Machine) (0) | 2023.04.27 |
| Chapter 3-4. 앙상블과 랜덤 포레스트 (0) | 2023.03.30 |





댓글