다양한 AutoEncoder
지난 챕터에서는 오토인코더의 개념과 가장 기본적인 형태인 적층형 오토인코더에 대해 알아보았다. 이 외에도 다양한 형태의 오토인코더가 존재한다. 이번 장에서는 몇 가지 인기있는 오토인코더에 대해 다루어본다.
Robust 오토인코더
Robust 오토인코더는 Robust PCA와 오토인코더가 결합된 오토인코더이다. 오토인코더는 이상이 포함된 데이터를 포함하여 학습시킬 경우 이상의 형태까지 학습될 수 있다. Robust 오토인코더는 이러한 문제점을 해결하기 위해 제안되었다. Robust 오토인코더를 이해하기 위해 먼저 Robust PCA에 대해 알아보자. 기존 PCA 방법은 이상치에 매우 민감하였다. 아래의 그림을 보자.
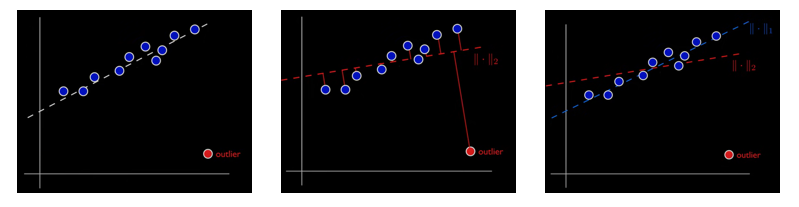
그림에서 파란 데이터는 정상 데이터를 붉은 데이터는 이상치를 나타낸다. 이상치가 없을 때 PCA를 진행하면 가장 왼쪽의 그림처럼 하얀 점선으로 특성을 잡는다. 하지만 데이터에 이상치가 존재하여 실제로 PCA를 진행하면 가운데 그림처럼 붉은 점선으로 특성을 잡게된다. Robust PCA는 이러한 이상치에 영향을 크게 받지 않는 강건한 PCA 기법이다. 가장 오른쪽 그림의 파란 점선이 Robust PCA를 통해 특성을 탐지한 결과이다.
Robust PCA는 데이터 X를 정제된 데이터인 L과 이상치(noise)인 S로 나눈다. 즉, X = L + S의 형태로 표현된다. Robust PCA는 아래의 최적화 식을 따른다. L의 손실항은 저차원으로 선형 투영하는 nuclear-norm의 형태임을 확인 할 수 있다. 또한, noise에 해당하는 S의 손실항은 L1 loss를 사용하고 있다.
$$ \underset{L,S}{min}\left\|L\right\|_{*}+\lambda \left\|S\right\|_{1} \qquad s.t. \quad \left\|X-L-S\right\|_{F}^{2}=0$$
Robust 오토인코더의 최적화 식도 Robust PCA의 최적화 식과 매우 유사하다. 다만, L의 손실 항에 실제 데이터와 재구축 데이터 L2 loss를 이용하였다. 아래는 Robust 오토인코더의 최적화식이다. E, D는 각각 인코더와 디코더를 의미한다.
$$ \underset{\theta }{min}\left\|L_{D} -D_{\theta}(E_{\theta} (L_{D}))\right\|_{2}+\lambda \left\|S\right\|_{1} \qquad s.t. \quad X-L_{D}-S=0$$
잡음 제거 오토인코더
잡음 제거 오토인코더는 시계열을 포함한 다양한 분야에서 이용되고 있지만, 특히 이미지 분야에서 활발하게 사용되고 있다. 이름에서 알 수 있듯이 데이터의 잡음을 제거하는 오토인코더로 가우시안 잡음이나 드롭아웃 층을 통하여 잡음이 섞인 데이터를 생성해준다. 이 데이터를 입력으로 받고 clean 데이터를 label로 이용하여 학습을 진행한다.

잡음이 포함된 MNIST 7 이미지를 입력하고 label로 clean 이미지를 주게 되면 오토인코더는 잡음을 제거하는 방법을 학습하게 된다. 따라서 잘 훈련된 잡음 제거 오토인코더는 잡음에 강건한 오토인코더이며 데이터 전처리에도 이용할 수 있다.
잡음제거 오토인코더의 구현은 간단하다. 일반적인 적층 오토인코더의 입력부분에 드롭아웃 층을 추가하면 된다. 아래는 28 by 28 데이터를 입력으로 받는 잡음 제거 오토인코더이다.

희소 오토인코더
일반적으로 오토인코더는 입력부분과 출력부분의 차원은 크게 하고 코딩영역의 차원을 작게 설계하여 데이터의 특성을 추출한다. 반면, 희소 오토인코더는 일반적인 오토인코더와 달리 코딩영역의 작은 차원을 통해 특성을 추출하지 않는다. 희소 오토인코더는 코딩영역 이전에 시그모이드 활성화 함수 층을 만들어 뉴런이 켜지거나 꺼지게 한다. 그리고 기존 손실함수에 코딩영역 뉴런이 켜져 있을 경우 페널티를 주는 항을 추가한다. 즉, 코딩영역의 손실함수를 통해 활성화된 뉴런의 수를 조절하여 특성을 추출한다.

희소 오토인코더도 28 by 28 데이터를 입력으로 받는 형태로 구현해보았다. 코딩영역의 크기가 300으로 이전 층보다 큰 것을 확인할 수 있다. 코딩영역에 시그모이드 활성화 함수를 넣어 뉴런의 on-off를 가능하게 했고 L1규제를 통해 활성화된 뉴런의 수를 희소하게 유지하도록 구성하였다. ActivityRegularization층은 입력을 그대로 반환하면서 훈련 손실에 입력의 절대값의 합을 더한다. 따라서 활성화된 뉴런의 수가 희소하게 유지된다. 이 층은 드롭아웃 층처럼 훈련을 할 때만 활성화된다.

변이형 오토인코더
변이형 오토인코더는 지금까지 다룬 오토인코더와 상당히 다르다. 가장 큰 특징은 생성적 오토인코더라는 점이다. 변이형 오토인코더를 이용하면 훈련 세트에서 샘플링 한 것과 유사한 데이터를 생성할 수 있다. 다른 특징은 확률적 오토인코더라는 것이다. 희소 오토인코더나 잡음 오토인코더와 달리 변이형 오토인코더는 훈련이 끝난 후에도 출력의 일부가 우연에 의해 결정된다.

변이형 오토인코더의 인코더는 입력 데이터의 평균과 표준편차를 찾는다. 이렇게 얻은 평균과 표준편차를 갖는 가우시안 잡음에서 샘플링한 데이터가 디코더에 입력된다. 즉, 훈련이 끝난 변이형 오토인코더는 코딩영역에 저장된 평균과 표준편차를 갖는 가우시안 잡음에서 샘플링되기 때문에 확률적 오토인코더의 특징을 갖으며 잡음이 디코딩된 출력은 실제 데이터와 유사하므로 생성적 오토인코더의 특징을 갖는 것이다.
손실함수는 두 부분으로 구성된다. 하나는 오토인코더의 입력을 재생산하도록 만드는 일반적인 재구성 손실이다. 다른 하나는 코딩을 간단한 가우시안 분포에서 샘플링한 것처럼 보이게 만드는 잠재 손실이다. 여기에는 가우시안 분포와 실제 코딩 분포 사이의 KL 발산을 이용한다. 실제 수식은 상당히 복잡하지만 다행히도 이는 아래와 같이 단순화할 수 있다. n은 코딩 차원, 벡터 μ와 σ는 각각 인코더의 평균, 표준편차 출력이다.
$$ L = -\frac{1}{2}\sum_{i=1}^{n}(1+log(\sigma _{i}^{2})-\sigma_{i}^{2}-\mu _{i}^{2}) $$
이를 그대로 이용하는 것도 가능하지만 수학적 안정성과 훈련의 속도를 높이기 위해 인코더가 σ가 아닌 σ 제곱에 로그를 취한 형태를 더 자주 사용한다.
$$ L = -\frac{1}{2}\sum_{i=1}^{n}(1+\gamma _{i}-exp(\gamma _{i})-\mu _{i}^{2}) $$
실습
Chapter 4-5.에서는 convolution layer로 이루어진 적층형 오토인코더를 이용하여 층간소음 시계열 데이터의 이상을 탐지했다. 이번 실습에서는 동일한 데이터 셋을 변이형 오토인코더를 이용해 이상탐지 해보자. 이전 실습과 동일하게 데이터 로드, 정규화, 전처리를 진행한다. 이제 변이형 오토인코더를 생성한자. 먼저, 평균과 표준편차를 입력하면 해당 가우시안 분포의 샘플을 반환하는 클래스를 생성하였다.

이어서 코딩 영역의 크기가 8인 변이형 오토인코더를 생성했다. 입력 데이터 형태인 (batch_size, 288, 1)에 맞추어주었으며 인코더를 통과한 값을 평균과 표준편차로 하여 Sampling 클래스를 이용해 샘플링하는 것을 확인할 수 있다. 디코더는 일반적인 오토인코더의 형태와 같다.
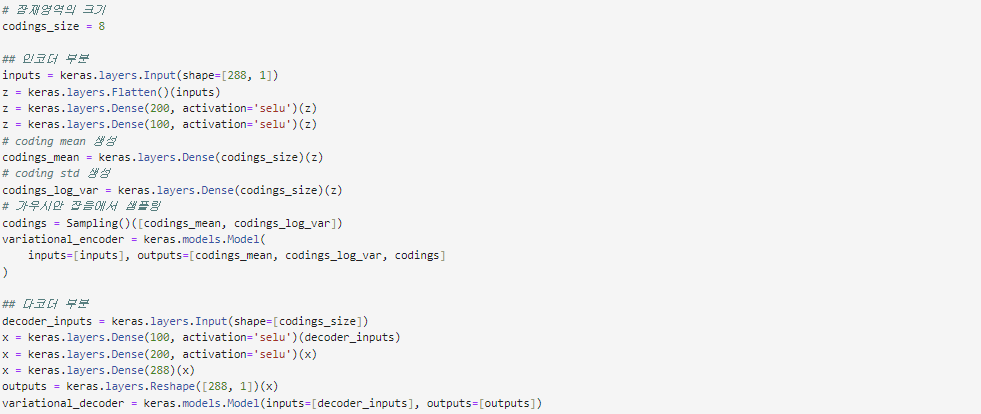
인코더와 디코더 부분을 연결하여 변이형 오토인코더를 완성했다. 위에서 소개했던 잠재손실을 손실함수에 추가했고 재구성 손실에는 mse를 이용했다. mse가 오차의 평균이므로 손실함수를 입력 데이터의 크기인 288로 나누어주는 것을 확인할 수 있다.

생성한 변이형 오토인코더 모델을 사용하여 학습했다. 이전 실습과 동일하게 첫번째 윈도우의 실제 데이터와 재구축한 데이터를 그래프로 나타내었다. 재구축 데이터가 실제 데이터를 어느정도 재현하였음을 확인할 수 있다. 아래 히스트그램은 학습 데이터 MSE 분포이다. 이 중 가장 큰 MSE인 0.27039를 THRESHOLD로 세팅하였다. 모든 실습 코드는 이전 Chapter 4-5. 오토인코더의 실습과 동일하다.

끝으로, 세팅한 THRESHOLD를 사용하여 이상을 탐지했다. MSE 분포를 통해 정상 데이터와 이상 데이터가 확연하게 구분되고 있은 것을 확인할 수 있다. 또한, 이상탐지 결과 그래프에서도 이상 데이터 부분이 정확하게 탐지된 것을 확인할 수 있다.

글 | AI기술연구2팀 임상오

'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 4-7. GAN(Generative Adversarial Networks) (0) | 2024.02.29 |
|---|---|
| Chapter 4-5. AutoEncoder (0) | 2023.12.27 |
| Chapter 4-4. Seq2Seq (0) | 2023.11.30 |
| Chapter 4-3. RNN (0) | 2023.10.26 |
| Chapter 4-2. 기초 베이지안 통계 (0) | 2023.09.21 |





댓글