Chapter 3-5. 서포트 벡터 머신 (Support Vector Machine)
서포트 벡터 머신은 선형/비선형 분류, 회귀, 이상치 탐색 등에 사용할 수 있는 다목적 머신러닝 모델이다. 분류 문제에 많이 쓰이며, 중간 크기의 데이터셋에 적합한 모델이다. 지금부터 서포트 벡터 머신의 이론에 대해 알아보고 실습을 통해 분류 및 회귀에서 어떻게 사용하는지 알아보자.

SVM의 아이디어와 자세한 수식 및 원리에 대해 분류 모델을 중심으로 먼저 알아보고, 회귀 모델의 원리에 대해 공부해보자. SVM의 기본 개념은 그림 1 와 같이 두 샘플 사이에 선을 그어, 그 선의 폭이 최대가 되도록 하여 두 샘플을 구분한다. 조금 더 자세히 설명하자면, 샘플이 특성을 정의하는 n 개의 변수들로 표현된다고 할 때, 샘플들은 n 차원 데이터 공간에 분포하게 된다. 서포트 벡터 머신의 목적은 n 차원의 데이터 공간에서 샘플 그룹들을 구분해 내는 최적의 분할선(optimal decision boundary)을 찾아내는 것이다. 이때, 서포트 벡터 머신과 선형 판별 분석의 다른점을 설명하자면, 선형 판별 분석은 선형 분할선을 찾아주지만, 서포트 벡터 머신은 커널 함수를 사용해 비선형 분할선도 찾아준다.
데이터 공간에서 샘플 그룹을 구분해주는 것을 초평면이라고 하는데, 이 초평면은 무수히 많이 존재한다. 이 때, 초평면과 가장 가까운 점과의 거리를 마진(margin)이라고 하는데, 각 초평면은 고유의 마진을 가진다. 그림 1 과 같이 점선과 실선의 마진 크기는 다르며, 실선을 최대 마진 초평면이라 부를 수 있고 이를 찾는 것이 SVM 의 목적이다.
SVM 에서 임의의 초평면에 대한 마진의 길이는 아래의 식에 의해 유도한다. 분할선은 초평면의 법선 벡터 W 와 편향 상수 b 에 의해 정의되며, 아래의 식을 갖는다.
$$ W^{T}X - b = 0 $$
이 분할선을 이용해 샘플 \(x_{i}\) 를 분리했을 때, 분할 선 위 또는 아래 영역에 있는지에 따라 그룹 변수 \(y_{i}\) 값은 +1 또는 -1 의 값을 가진다. 초평면 위에 있는 초평면과 가장 가까운 샘플을 \(x^{+}\), 초평면 아래에 있는 초평면과 가장 가까운 샘플을 \(x^{-}\) 라 할 때, 각각의 샘플은 아래의 식을 만족한다.
$$ W^{T}X^{+} - b = +1 $$ $$ W^{T}X^{-} - b = -1 $$
위의 조건식에서 \(X^{+}\) 와 \(X^{-}\) 를 지나는 초평면과 평행한 두개의 초평면 사이의 거리인 마진은 위의 두식을 빼서 구할 수 있다. 그러면 아래와 같은 식을 얻는다. $$ margin = \left \| X^{+} - X^{-} \right \| = \frac{2}{\left \| w \right \|} $$ $$ max \frac{2}{\left \| w \right \|} \Leftrightarrow min \frac{\left \| w \right \|}{2} $$
최대의 마진을 찾기 위해서는 w의 최솟값을 찾아야 한다. 또한, \(y_{i}\)=1인 샘플은 \(W^{T}X_{i}\geq\) 1 이며, \(y_{i}\) = -1인 샘플은 \(W^{T}X_{i}\leq\) 1 이므로 아래의 제약조건을 만족해야 한다. $$ y_{i}(W^{T}X_{i}-b) \geq 1 $$
W의 최소화 문제는 아래의 라그랑주 승수법을 이용해 최적의 w, b 값을 구할 수 있다.
$$ L(w, b,\lambda) = \frac{1}{2}w^{T}w - \sum_{i=1}^{N}\lambda y_{i}w^{T}x_{i} + \lambda N $$ $$ = \lambda N - \frac{1}{2}w^{T}w $$ $$ = \lambda N - \frac{\lambda^{2}}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}(y_{i}x_{i})^{T}(y_{i}x_{i}) $$
위의 식에서 \(x_{i}\) 와 \(y_{i}\) 를 대입하고 L 값을 최대화하는 \(\lambda\) 를 구한 후, \(\frac{dL}{dw} = 0\) 을 이용해 w 를 구하고 \(W^{T}X^{+} - b = \pm 1\) 을 이용해 b 값을 구한다.
앞에서 유도한 SVM 은 선형 SVM 이다. 선형 SVM 은 샘플 분할 경계가 복잡한 경우 분류 성능이 떨어진다는 한계를 가진다. 커널이라는 매핑 함수를 통해 비선형, 비모수 분할선을 정의함으로 이를 해결한다. 많이 쓰이는 커널 함수를 소개하자면 아래와 같다.
$$ 선형 : K(a, b) = a^{T}b $$ $$ 다항식 : K(a, b) = (\gamma a^{T}b + r)^{d} $$ $$ 가우시안 RBF : K(a, b) = exp(-\gamma \left \| a - b \right \|^{2}) $$ $$ 시그모이드 : K(a, b) = tanh(\gamma a^{T}b + r) $$
지금까지 서포트 벡터 머신의 이론에 대해 알아보았다. 이제부터 예제를 통해 SVM 선형 분류, SVM 비선형 분류, SVM 회귀를 실습해 보자. 실습 데이터는 sklearn 의 iris 데이터를 사용한다.
선형 SVM 분류
모든 샘플이 도로 바깥쪽에 올바르게 분류되어 있다면 이를 하드 마진 분류라고 한다. 하드 마진 분류는 선형적으로 구분 될 수 있어야 제대로 작동하고 이상치가 있다면 하드 마진을 찾을 수 없을 수도 있다. 반대로 도로의 폭을 가능한 넓게 유지하고 마진 오류 사이에 적절한 균형을 잡은 것을 소프트 마진 분류라고 한다. 사이킷런에서는 C 라는 하이퍼파라미터를 통해 마진 오류를 조정한다. 일반적으로 마진 오류가 작은 것이 좋으나 일반화가 잘 되는지를 우선적으로 고려해야한다. 또한, SVM 모델이 과대적합이라면 C 를 감소시켜 모델을 규제할 수 있다.
SVM 모델 분류 예측
In[1]:
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.svm import LinearSVC
# iris 데이터 로드를 진행하고, 꽃잎 길이와 너비만 추출해보자.
iris = datasets.load_iris()
X = iris['data'][:, (2, 3)]
y = (iris['target'] == 2).astype(np.float64)
# SVM 모델 설정
svm_clf = Pipeline([("scaler", StandardScaler()), ("linear_svc", SVC(C=1, kernel='linear'))])
# 모델 훈련
svm_clf.fit(X, y)
# 모델 예측
svm_clf.predict([[5.5, 1.7]])
Out[1]:
array([1.])
간단하게 SVC 함수로 C=1, kernel='linear' 로 값을 에측한 결과, 1, 즉 virginica 로 예측한 것을 알 수 있다. 다음은 C 의 값을 다르게 하여 SVM 마진을 계산하여 보자. 아래 코드에서의 C 값은 penalty 라는 객체로 표현하였고, sklearn 공식 페이지에서의 예시 중 하나이다.
In[2]:
# Code source: Gaël Varoquaux
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from sklearn import svm
# 40개의 포인트를 생성
np.random.seed(0)
X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
Y = [0] * 20 + [1] * 20
# figure number 지정
fignum = 1
# 모델 훈련
for name, penalty in (("unreg", 1), ("reg", 0.05)):
clf = svm.SVC(kernel="linear", C=penalty)
clf.fit(X, Y)
# 초평면 설정
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-5, 5)
yy = a * xx - (clf.intercept_[0]) / w[1]
# 마진의 크기를 설정하자
margin = 1 / np.sqrt(np.sum(clf.coef_**2))
yy_down = yy - np.sqrt(1 + a**2) * margin
yy_up = yy + np.sqrt(1 + a**2) * margin
# 그래프 그리기
plt.figure(fignum, figsize=(18, 12))
plt.clf()
plt.plot(xx, yy, "k-")
plt.plot(xx, yy_down, "k--", color="blue")
plt.plot(xx, yy_up, "k--", color="blue")
plt.scatter(
clf.support_vectors_[:, 0],
clf.support_vectors_[:, 1],
s=80,
facecolors="none",
zorder=10,
edgecolors="red",
cmap=cm.get_cmap("RdBu"),
)
plt.scatter(
X[:, 0], X[:, 1], c=Y, zorder=10, cmap=cm.get_cmap("RdBu"), edgecolors="k"
)
plt.axis("tight")
x_min = -4.8
x_max = 4.2
y_min = -6
y_max = 6
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
fignum = fignum + 1
plt.show()
Out[2]:

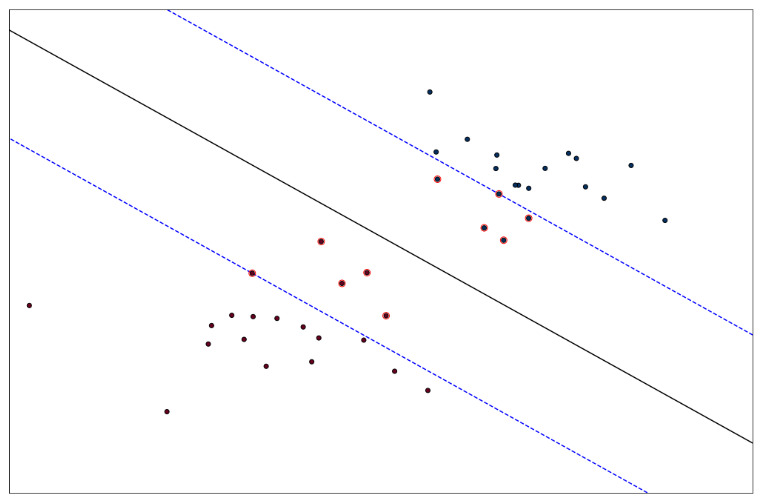
앞서 말했듯이, C=0.05 일 때, 마진 오류가 높을 수 있지만 일반화가 더 잘된다. 만약 비선형 SVM 분류를 하고 싶다면, from sklearn.svm import SVC 이후 모델 생성 시 SVC(kernel='poly') 처럼 kernel 함수만 따로 설정해주면 되므로 실습은 생략한다. 이제 SVM 회귀에 대해 알아보자.
SVM 회귀
SVM 회귀의 원리는 분류의 목표와 반대라고 할 수 있다. 일정한 마진 오류 안에서 두 클래스 간의 도로 폭이 가능한 한 최대로 하는 분류와는 반대로, 제한된 마진 오류 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 학습한다. 이 때, 도로의 폭은 하이퍼파라미터 \(\epsilon\) 으로 조절한다. 임의로 데이터를 생성하여 회귀식을 만들어보자.
In[3]:
from sklearn.svm import LinearSVR
# 데이터 생성
np.random.seed(42)
m = 100
X = 3 * np.random.rand(m, 1)
y = (8 * 3 * X + np.random.randn(m,1)).ravel()
# 모델 훈련
svm_reg = LinearSVR(epsilon=1.5, random_state=42)
svm_reg.fit(X, y)
# 서포트 벡터 함수 지정
def find_support_vectors(svm_reg, X, y):
y_pred = svm_reg.predict(X)
off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
return np.argwhere(off_margin)
svm_reg.support_ = find_support_vectors(svm_reg, X, y)
# 그래프 그리기
def plot_svm_regression(svm_reg, X, y, axes):
y_pred = svm_reg.predict(X)
plt.figure(figsize=(16, 12))
plt.plot(X, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
plt.plot(X, y_pred + svm_reg.epsilon, "k--", color="red")
plt.plot(X, y_pred - svm_reg.epsilon, "k--", color="red")
plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
plt.plot(X, y, "bo")
plt.xlabel(r"$x$", fontsize=18)
plt.ylabel(r"$y$", fontsize=18)
plt.legend(loc="upper left", fontsize=18)
plot_svm_regression(svm_reg, X, y, [0, 3, 5, 16])
plt.title(r"$\epsilon = 1.5$", fontsize=18)
plt.show()
Out[3]:

SVM 회귀 역시 SVM 분류와 마찬가지로 kernel 트릭으로 비선형 회귀가 가능하다. LinearSVR 대신 from sklearn.svm import SVR 이후 모델 생성 시 SVR(kernel="poly")로 kernel 함수를 지정해 주면 된다.
이렇듯, SVM 의 Epsilon 값을 작게 하여 마진을 작게도 만들어보고, 비선형 분류 및 회귀 모델도 자율적으로 실습해보면, 필요한 데이터에 적용하여 유용하게 쓸 수 있을 것이다.
글 | AI모델연구팀 김경준

'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 3-7. GAM 이론 및 실습 (0) | 2023.06.29 |
|---|---|
| Chapter 3-6. 차원 축소 (0) | 2023.05.25 |
| Chapter 3-4. 앙상블과 랜덤 포레스트 (0) | 2023.03.30 |
| Chapter 3-3. 결정 트리 (0) | 2023.02.22 |
| Chapter 3-2. 모델 훈련 (0) | 2023.01.19 |





댓글