Chapter 3-3. 결정 트리
결정 트리는 트리 구조를 기반으로 데이터에서 규칙을 학습하여 분류(Classification) 문제와 회귀(Regression) 문제, 그리고 다중출력 문제까지도 해결할 수 있는 지도학습 계열의 머신러닝 알고리즘이다.
결정 트리 모델은 나무가 가지를 엮은 것과 같은 구조로 (마치 스무고개 처럼) 복잡한 데이터에서도 빠르게 동작하는 것이 큰 특징이며, 널리 알려진 머신러닝 알고리즘 중 하나인 랜덤 포레스트(Random Forest)의 기본 구성이 되는 모델이다.
결정 트리(Decision Tree)
결정 트리는 특정 기준(질문) 을 따라 데이터를 구분 짓는다. 결정 트리의 가장 첫 번째 기준은 트리에서 최초 깊이인 루트 노드(Root node) 에서 시작한다. Python 의 머신러닝 라이브러리인 'Sklearn' 에서는 결정 트리를 이진 트리로만 구성하는 'CART(Classification and Regression Tree) 알고리즘' 사용하여 매번 노드의 분기마다 데이터를 두 개의 영역으로만 구분하게 된다.
트리가 하위 깊이로 깊어지면서 생성되는 새로운 분류 기준이 되는 질문을 노드(Node) 라고 말하며, 더 이상 분기가 되지 않는 마지막 노드를 'Terminal' 또는 'Leaf Node' 라고 칭한다.
결정 트리는 다른 알고리즘에 비해 데이터의 전처리가 거의 필요하지 않다는 장점과 학습 데이터에서 서로 다른 특성 값들의 범주를 조정하는 Feature Scaling 작업이 따로 필요하지 않는다. 이렇듯 결정 트리는 매우 직관적이며, 결과 및 결정 방식에 대한 해석과 이해가 쉬워 "화이트 박스" 모델에 속하는 알고리즘이기도 하다.

| Root Node | 남자인가? |
| intermediate Node | (나이가 > 9.5) 인가? or (sibsp > 2.5) 인가 ? |
| Terminal or Leaf Node | 생존 or 사망 |
결정 트리 알고리즘의 프로세스
결정 트리 알고리즘의 동작 순서를 다음 그림을 통해 이해해보자.

1. 가장 첫 번째 기준이 되는 "Root Node" 에서는 데이터를 가장 잘 구분 지을 수 있도록 기준 생성하고, 데이터를 나눈다.

2. Root Node 분기에 이어서, 각각 새로운 기준으로 데이터의 구분짓는다.
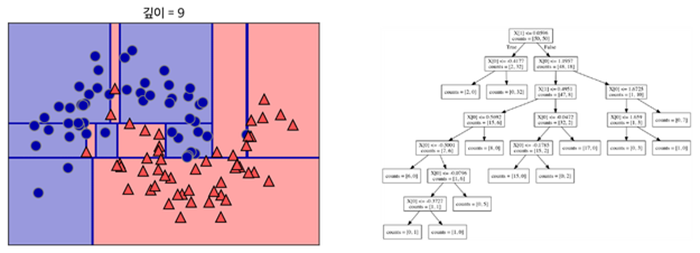
3. 위와 같은 방식을 반복하며 트리 깊이는 점점 깊어지는 형태로 구성된다.
결정 트리에 어떠한 규제가 없이 (즉 알고리즘의 파라미터에 대한 조정 없이) 모델링 한다면 3번 그림과 같은 결정 트리 모델이 생성되고, 이를 보통 과대적합(overfitting) 문제가 발생했다고 말할수 있다.
훈련 데이터에 대한 과대적합 문제를 피하기 위한 방법으로 결정 트리에서는 가지치기(Pruning) 라는 기법이 있다.
가지치기란 나무에서 가지를 치는 작업과 같이 결정 트리 알고리즘의 파라미터 규제를 주어 트리의 최대 깊이, 노드 분할의 최소 데이터 수 등을 제한시켜 과대적합 문제를 피하도록 모델을 설계하는 방법이다.
아래에는 Sklearn 에서 지원하는 DecisionTree 알고리즘의 주요 파라미터 목록과 설명이 있다.
| Parameter | Description |
| max_depth | 트리의 최대 깊이 제한, 감소시킬수록 과대적합의 위험이 줄어든다. |
| max_features | 각 노드에서 분할에 사용할 features 개수 |
| min_sample_split | 분할되기 위한 최소 샘플 수 조건 |
| min_sample_leaf | 리프 노드가 가져야할 최소 샘플 수 |
| min_weight_fraction_leaf | min_sample_leaf 와 동일 (가중치가 부여된 전체 샘플에서의 비율) |
| max_leaf_node | 리프 노드의 최대 수 |
| min_impurity_decrease | 분할로 얻어질 최소한의 불순도 감소량 |
지니 불순도와 엔트로피
결정 트리 알고리즘 파라미터 조정을 위해 알아야하는 개념 중엔 "criterion" 이라는 매개변수가 있다.
이는 트리의 분할에 대한 기준을 정하는 것으로 기본 옵션으로 '지니 불순도' 가 사용되며, 다른 옵션으로는 '엔트로피 불순도' 가 사용될 수 있다. 여기서 불순도가 의미하는 것은 무엇인지, 엔트로피란 무엇인지에 대해 아래 관련된 그림을 보며 알아보자.

"불순도"라는 것은 다양한 범주에서 개체들의 무질서함을 측정하는 지표로 해석할 수 있다.
일반적으로 분류(Classification) 문제에서 사용될 수 있으며, 서로 다른 집단에 속하는 데이터들의 불균형함을 측정한다.
"지니 불순도" 란 정답이 아닌 다른 라벨이 뽑힐 확률이라고 정의된다.
예를 들어 위 그림과 같이 빨간 구슬-파란 구슬의 데이터를 한 집단으로 묶었을 경우, 파란 구슬만 담긴 집단의 지니 불순도는 0 이고 마찬가지로 빨간 구슬만 담겨 있는 집단의 지니 불순도는 0 이다.
하지만 파란 구슬 절반, 빨간 구슬 절반으로 정확히 구성되는 집단에서의 불순도는 1로 최대 확률 값을 가지게 된다.
"엔트로피" 란 열역학에서 파생된 용어로 불순도를 수치적으로 나타낸 척도이다.
지니 불순도와 동일한 의미로 해석되지만, 차이점으로는 계산식에 로그 계산이 포함되어 있다. 엔트로피가 높다는 것은 불순도가 높아서 데이터가 균형있게 잘 구성되어 있음을 의미하고, 엔트로피가 낮은 것은 불순도가 낮고 하나의 데이터 분류로만 구성되어 데이터가 불균형하다는 것을 의미한다.
학습 진행 방향성
결론적으로 결정 트리 알고리즘은 엔트로피가 최소, 즉 불순도를 0에 가깝게 만드는 방향으로 학습을 진행하게 된다.
첫 번째 기준(질문)인 Root Node 에서 데이터를 두 그룹으로 나누는데, 불순도가 0에 가깝게 기준을 설정한다는 것을 의미한다. 최대한 파란 구슬만 있는 집단으로 최대한 빨간 구슬만 있는 집단으로 분류하는 것이 목표이다.
결정 트리 알고리즘은 앞서 얘기한 바와 같이 데이터 전처리 (정규화, 결측치, 스케일링 등) 를 하지 않아도 되고, 빠르게 동작하며 모델의 추론 결과에 대한 해석이 가능하다는 장점으로 빠르게 적용해볼 수 있는 알고리즘이다. 하지만 쉽게 과적합 문제에 빠질 수 있고, 데이터 샘플 수가 증가할수록 알고리즘의 효율성이 떨어지는 단점들도 존재한다.
결국 결정 트리의 알고리즘을 적용하기에 앞서 우리가 사용하고자하는 데이터에 대한 면밀한 분석과 명확한 목적에 맞는 적절한 규제(파라미터 튜닝)가 동반되어야만 올바른 모델을 활용할 수 있을 것이다.
* 이미지 출처:
기획 및 글 | AI기술연구팀 유용빈

'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 3-5. 서포트 벡터 머신 (Support Vector Machine) (0) | 2023.04.27 |
|---|---|
| Chapter 3-4. 앙상블과 랜덤 포레스트 (0) | 2023.03.30 |
| Chapter 3-2. 모델 훈련 (0) | 2023.01.19 |
| Chapter 3. 머신러닝 (0) | 2022.11.23 |
| Chapter 2-3. 기초 시계열 분석 (0) | 2022.10.26 |





댓글