Chapter 3. 머신러닝
머신러닝의 정의와 활용
머신러닝이란 무엇인가? 머신러닝(Machine Learning)은 인공지능(Artificial Intelligence)의 한 부분으로, 입력된 데이터로부터 컴퓨터가 학습하도록 프로그래밍하는 것을 말한다. 이 챕터에서는 머신러닝을 분류하는 두 가지의 방법에 대해 알아볼 것이다.
* 머신러닝을 분류하는 첫 번째 방법: 지도 학습, 비지도 학습, 준지도 학습, 강화 학습
지도 학습(Supervised Learning)은 훈련 데이터에 레이블(정답)이 있는 학습 방법이며, 대표적으로 K-nearest neighbors(K-최근접 이웃), Linear regression(선형 회귀), Logistic regression(로지스틱 회귀), Support vector machine(SVM, 서포트 벡터 머신), Decision tree(결정 트리), Random forest(랜덤 포레스트), Neural networks(신경망) 등이 있다. 아래 그림을 예로 들자. 기린(정답)과 고양이(정답)의 이미지를 잘 훈련한 알고리즘은 기린 이미지를 보았을 때 기린이라고 판단할 것이고, 고양이의 이미지를 보았을 때에는 고양이로 판단할 것이다.

반대로 비지도 학습(Unsupervised Learning)은 훈련 데이터에 레이블(정답)이 없는 학습 방법으로, 크게 군집, 차원 축소 등이 있다. 군집(Clustering)은 비지도 학습에 있어서 널리 쓰이는 알고리즘 중 하나인데, k-means(K-평균), DBSCAN, Hierarchical cluster analysis(HCA), Isolation forest 등이 있다. 위에서 든 예와 다르게 기린과 고양이가 레이블이 되어있지 않은 데이터에서 비지도 학습 알고리즘은 기린 혹은 고양이의 특성을 추출해서 분류를 한다.
예를 들면, 기린의 노란색, 얼룩, 목부분의 긴 특성들을 가지고 알고리즘은 이것이 '기린'인지는 모르지만 '노랗고 얼룩이 있으며 목이 긴 동물'로 분류할 것이다. 같은 개념으로 비지도 학습을 한 알고리즘은 '고양이'인지는 모르지만 '꼬리가 길고 귀가 뾰족한 동물'로 분류할 것이다.
이와 관련하여 차원 축소, 주성분 분석(Principal Component Analysis, PCA), 커널 PCA 등이 있는데, 이는 추후 Chapter 3-2. 비지도 학습 부분에서 심층적으로 다룰 것이다.

특정 알고리즘은 일부만 레이블이 되어있는 데이터를 다룰 수 있다. 이런 학습 방법을 준지도 학습이라 하는데, 비지도 학습 중 군집에서도 쓰일 수 있다. 예를 들어 무수히 많은 동물 중, 토끼와 거북이는 레이블이 되어있다고 가정하자. 어느 지역에 동물원 A와 동물원 B가 있을 때, 알고리즘은 토끼와 거북이가 동물원 A와 동물원 B 중에 어느 곳에 있는지 자동으로 인식할 수 있다.
강화 학습이란, 어떤 에이전트(학습하는 시스템)가, 환경(Environment)을 관찰하며, 행동(Action)을 실행하고, 그 결과로 보상(Reward)을 받는다. 여기서의 보상은 긍정/부정적인 형태이며, 부정적인 보상은 벌점(Penalty)이라 표현한다. 2017년 5월에 있었던 바둑 로봇 알파고와 인간의 대결이 대표적인 예로, 알파고는 세계 챔피언과 겨루기 위해 그동안 수많은 학습을 하여 승리 전략을 만들었다.
머신러닝을 다른 방법으로 분류한다면 오프라인 학습과 온라인 학습으로 나눌 수 있다.
오프라인 학습은 배치 학습(Batch learning)이라고도 부르는데, 이는 시스템이 점진적으로 학습할 수 없다. 학습 가능한 데이터를 모두 학습한 후, 그것을 적용하여 더 이상의 학습 없이 실행된다. 만약 학습 데이터가 더 생긴다면, 전체 데이터로 업데이트한 후에 시스템에 변화를 줄 수 있다.
예를 들어 시계열 데이터에선 매 분, 혹은 매일 새로운 데이터가 들어온다. 이런 데이터에는 배치 학습이 적합하지 않다고 볼 수 있다. 또한, 데이터의 양에 따라 CPU, 메모리 공간, 디스크 공간 등 많은 컴퓨터 자원이 필요하다는 점이 단점이다.
반대로 온라인 학습은 미니 배치(Mini-batch)라는 작은 묶음 단위로 데이터를 주입하여 시스템을 훈련한다. 데이터의 양은 한 개부터, 미니 배치 사이즈에 따라 들어오는데, 이는 학습 단계를 빠르게 할 수 있는 장점이 있으며 앞서 말한 배치 학습과 다르게 컴퓨터 자원이 적게 든다. 온라인 학습에서 중요한 파라미터 중 하나는 학습률이다.
학습률이란?
학습률은 데이터에 적응하는 속도를 정하는데, 학습률이 높을수록 빠르게 적응하지만 예전 데이터를 금방 잊는다. 예를 들어, 학습률이 높은 지도 학습에서 최근에 등록된 보이스피싱 전화번호만 걸러진다면 학습률을 낮춰야 한다.
온라인 학습은 들어오는 데이터를 모니터링하는 것이 중요하다. 만약 알고리즘의 성능이 감소되면, 그것은 나쁜 데이터가 주입되고 있다는 뜻이기에 학습을 즉각 중단시켜야 한다. 여기서 나쁜 데이터는 이상치라 설명할 수도 있는데, 이는 이상치 탐지 알고리즘을 사용하여 걸러 낼 수도 있다.
오프라인 / 온라인 학습으로 분류하는 방법에 이어 머신러닝은 어떻게 일반화되는가에 따라 분류할 수 있다. 일반화하는 학습법에는 사례 기반 학습과 모델 기반 학습이 있다.
사례 기반 학습(Instance-based learning)에는 대표적으로 K-최근접 이웃(K-nearest neighbors) 회귀 방법이 있다. K-최근접 이웃 기법에는 유클리드 거리 기법 혹은 이진 속성으로 유사도 지표를 설명할 수 있다.
예를 들면, 어느 기업의 주가 예측을 하기 위해 재무비율 평가를 한다고 하자. 재무비율 중 주가 순자산비율(PBR), 매출액 순이익률(ROS), 주가 보상률(PER)을 반영한다고 할 때, 이 세 데이터를 3차원의 공간상에 투영한 후 우리는 정답을 도출해 낼 수 있다. 이를 유클리드 거리 기법이라 부른다. 다른 방법은 이진 데이터로 유사도 지표의 정확성을 높이는 것이다. 데이터의 특성이 0, 1 혹은 예, 아니요로 표현이 가능하다면 예측성능을 평가해 볼 수 있다.
모델 기반 학습(Model-based learning)은 알고리즘 모델을 만들어 예측(Prediction)을 통해 일반화한다. 우리는 모델의 효용 함수(Utility function)나 비용 함수(Cost function)로 성능을 평가할 수 있는데, 모델을 만들 때 최상의 성능을 낼 수 있도록 목표한다.
효용 함수(Utility function)란?
적합도 함수(Fitness function)라고도 정의하며, 모델이 얼마나 제공된 데이터에 좋은지(Fit) 측정하는 함수이다.
비용 함수(Cost function)란?
입력 데이터에 대한 오차를 계산하는 함수를 비용 함수라 한다. 모델이 얼마나 제공된 데이터에 나쁜지를 측정하는 함수이다. 여기서 비용 함수와 손실 함수를 헷갈리면 안 된다. 손실 함수(Loss function)는 입력 데이터에 대한 예측값과 실제값의 오차를 계산하는 함수이다. 따라서 데이터 셋에 대한 손실 함수의 평균으로 우리는 비용 함수를 추출해 낼 수 있다. 비용 함수가 손실 함수보다 상위 개념으로 이해하면 된다.
지금까지 머신러닝을 분류하는 방법들을 알아보았다. 머신러닝 기법들에 대해 자세히 공부하며 실습 예제를 다뤄 보기 전에, 머신러닝 이후에 딥 러닝 모델을 만들 때 우리는 알고리즘의 성능이 좋지 않은 건지, 데이터가 좋지 않은 건지 판단하며 진행해야 한다.
데이터가 좋지 않을 때를 먼저 살펴보자. 데이터가 좋지 않다고 판단하는 기준에는 충분하지 않은 훈련 데이터의 양, 대표성이 없는 훈련 데이터가 있다. 머신러닝 알고리즘이 강아지와 고양이를 구분한다고 하자. 만약 강아지 혹은 고양이 사진(데이터)이 충분하지 않으면, 알고리즘이 강아지나 고양이를 쉽게 정의 내리지 못할 것이다. 강아지에 대한 종류가 20개라고 가정했을 때, 한 종류만 학습한 알고리즘은 다른 종류의 강아지를 강아지라 판단하지 못할 가능성이 높다.
우리는 데이터에 대표성이 없을 때에도 데이터가 좋지 않다고 말한다. 예를 들어, 민주주의 국가 중 GDP(Gross Domestic Product) 순으로 나열한다 하였을 때, 공산주의 국가만 있는 데이터 셋으로 GDP 그래프를 생산한다면 안될 것이다. 각 나라를 샘플이라 표현할 수 있는데, 이때 우리는 샘플링 잡음(Sampling noise)을 설명할 수 있다. 샘플링 잡음이란, 샘플의 수가 적으면서 대표성이 없는 데이터가 포함되어 있는 것을 말한다. 샘플의 수가 적을수록 샘플링 잡음이 크고 정밀성(Precision)이 낮다고 설명한다. 반대로, 샘플의 수가 크지만 대표성이 없는 데이터가 대부분인 경우를 샘플링 편향(Sampling bias)이 있다 말한다.
머신러닝 혹은 딥 러닝을 공부할 때 많이 나오는 용어 중, 나쁜 알고리즘의 예시로 모델의 과대 적합(Overfitting)과 과소 적합(Underfitting)이 있다.
과대 적합이란, 적은 표본으로 지나친 일반화를 했을 때라고 이해하면 된다. 머신 러닝에서의 과대 적합은 모델이 훈련 데이터에 잘 맞았지만 일반성은 없다는 것이다. 모델이 과대 적합의 양상을 보인다면, 모델을 단순화하기 위해 규제(Regularization)를 가하거나, 자유도(Degree of freedom)를 알고리즘에 부여한다.
규제와 자유도 모두 학습 알고리즘에 부여하는데, 규제의 양은 하이퍼 파라미터(Hyperparameter)가 정한다. 하이퍼 파라미터의 종류는 알고리즘마다 다른데, 이는 곧 학습 알고리즘의 파라미터이다. 하이퍼 파라미터는 모델을 지칭하는 것이 아니기 때문에, 학습하기 전에 지정되어야 하고, 훈련하는 동안에는 상수로 남는다. 머신러닝 혹은 딥러닝 모델을 만들 때 하이퍼 파라미터 튜닝은 매우 중요하다.
한편 과소 적합이란, 과대 적합과 반대로 모델이 데이터의 구조를 학습하지 못할 정도로 단순할 때 발생한다. 과소 적합을 해결하기 위해 우리는 모델의 제약(규제 하이퍼 파라미터)을 줄이거나, 파라미터가 더 많은 강력한 모델로 변환한다.
지금까지 우리는 모델이 얼마나 훈련 데이터 셋에 정밀성이 높게 학습하는지 판단하는 기준에 대해 알아보았다. 모델이 테스트 데이터 셋, 즉 앞으로 모델에 들어오는 새로운 샘플에 잘 일반화하는지 판단하기 위한 기준을 설명하겠다.
내가 만든 모델이 새로운 샘플에 잘 맞는지 성능을 판단하는 기준에는 RMSE, SMAPE, F1 SCORE, 등이 있는데, 이는 추후에 자세히 알아보도록 하겠다.
현재 XAIOps의 알고리즘 성능(정확도)을 평가할 때 이런 기준들을 모두 이용하고 있다. 예를 들어 XAIOps에서의 RMSE(Root-Mean-Squared-Error)는 교차검증 구간의 예측값과 실제값을 비교하여 예측 알고리즘이 얼마나 정확하게 예측했는지 평가할 때 쓰인다. 이러한 성능지표를 확인하기 위하여 우리는 먼저 훈련 데이터를 훈련 세트와 테스트 세트로 나누어야 한다. 전체 훈련 데이터에서 일반적으로 30% 정도를 테스트 세트로 지정한다. 이를 검증 세트(Validation set)이라 한다. 나머지 70%를 훈련하여 30%를 예측한 후, 30%의 실제값과 예측값을 비교하는 것을 교차 검증(Cross-validation)이라 한다. 여기서 70%의 데이터 셋으로 훈련할 때, 우리는 앞서 알아보았던 하이퍼 파라미터를 튜닝하여 가장 성능이 좋은 것을 선택한다.
교차 검증하는 방법에는 K-Fold 교차 검증이라는 방법도 있는데, 이는 K 개의 Fold(단위)를 만들어 진행하는 방법이다. 아래 그림을 참조하도록 하자.
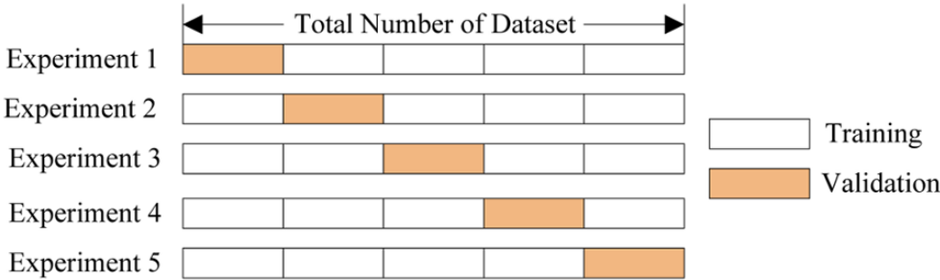
기존 교차검증과 같이 훈련 세트와 테스트 세트를 나눈다. 위 그림에서는 5개의 Fold로 나누었지만, 데이터 크기에 따라 Fold의 개수를 정하면 된다. 훈련 세트의 범위를 바꾸면서 테스트 세트의 범위를 바꿔 지정하며 교차검증을 K번 반복하여 진행하면 된다.
한 가지 단점은 일반적인 교차검증보다 시간 소요가 크다는 점이지만, 각각의 Fold에서 도출된 에러 값의 평균으로 우리는 최적의 하이퍼 파라미터를 구함으로써 최고의 성능을 내는 모델을 찾을 수 있다.
지금까지 우리는 머신러닝이 무엇이고, 분류 방법에 따라 알고리즘의 종류에 대해 살펴보았으며 알고리즘의 성능을 검증하는 방법까지 알아보았다. 다음 장에서는 알고리즘을 훈련(학습)할 때 중요한 몇 가지 개념들에 대해 공부해보도록 하자.

기획 및 글 | AI 모델팀 김경준
'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 3-3. 결정 트리 (0) | 2023.02.22 |
|---|---|
| Chapter 3-2. 모델 훈련 (0) | 2023.01.19 |
| Chapter 2-3. 기초 시계열 분석 (0) | 2022.10.26 |
| Chapter 2-2. 시계열 데이터 전처리 (0) | 2022.09.28 |
| Chapter 2. Pandas 3편 : Time Series 머신러닝을 위한 Python 필수 라이브러리 (0) | 2022.08.25 |





댓글