Time Series 머신러닝을 위한 기초 선형대수 및 통계학
머신러닝과 딥러닝 공부를 시작하고 싶은 분들을 위해, 여러 분야 중 시계열 데이터를 활용한 데이터 처리 및 머신러닝, 딥러닝 알고리즘을 소개하고자 한다. 이는 엑셈의 AI 기반 IT 운영 지능화 솔루션인 XAIOps의 알고리즘 모델들에 대해 이해할 수 있는 첫 걸음이기도 하다. 학습이 모두 끝난 후에는 머신러닝과 딥러닝이 무엇이며, XAIOps의 알고리즘들이 어떤 방식으로 모델링 되는지에 대한 기초적 이해에 도움이 될 것이다. 이에 앞서 데이터 처리 및 AI 알고리즘을 이해하기 위해 사전 지식으로 요구되는 기초 선형대수 및 통계학에 대해 알아보자.
우리는 왜 행렬을 공부해야 할까? 많은 양의 데이터(행렬) 구조를 변환할 때, 알고리즘(모델)의 학습 시간을 줄이고, 메모리 사용량과 같은 자원을 적게 소비할 수 있기 때문이다.
행렬을 공부하기 전에 알아야 할 개념은 텐서이다. 기본적으로 크기만 가진 스칼라를 0차원 텐서, 숫자를 배열한 벡터를 1차원 텐서, 행렬을 2차원 텐서, 앞으로 다룰 시계열 데이터를 3차원 텐서로 나타낸다. 먼저, 2차원 텐서인 행렬에 대해 먼저 살펴보자.
1-1. 기초 행렬
시계열(Time Series) 데이터는 주로 ‘데이터 테이블(Data table)’ 형태로 표현되어 있다. 이는 행렬(matrix)의 형태로 표현이 가능하다. 이름 그대로, 행(row)과 열(column)의 데이터로 구성되어 있다고 보면 된다. 행렬로 표현된 데이터를 효율적으로 다루기 위해 기초 행렬에 대한 이해는 필수이다.
행렬의 기본 원소 표기법은 \(a_{ij}\) (i: 행 번호, j: 열 번호)이다. 예를 들면, 우리는 i=3, j=4인 행렬을 3(three) by 4(four) matrix라 표현한다. $$\begin{bmatrix} a_{11} &a_{12} &a_{13} &a_{14} \\ a_{21} &a_{22} &a_{23} &a_{24} \\ a_{31} &a_{32} &a_{33} &a_{34} \\ \end{bmatrix}$$
▲ 대각 행렬(D): 행렬의 대각 원소를 제외한 모든 성분이 0인 행렬
$$D = \begin{bmatrix} 4& 0& 0\\ 0& 5& 0\\ 0& 0& 6\\ \end{bmatrix}$$
▲ 단위 행렬(I): 행 번호와 열 번호가 같은 원소만 1이며, 그 외의 모든 성분이 0인 행렬
$$I = \begin{bmatrix} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ \end{bmatrix}$$
▲ 전치 행렬: 기존 행렬에서의 행과 열을 바꾼 행렬
\(A = \begin{bmatrix} a_{11} &a_{12} &a_{13} &a_{14} \\ a_{21} &a_{22} &a_{23} &a_{24} \\ a_{31} &a_{32} &a_{33} &a_{34} \\ \end{bmatrix}\) 라 표현했을 때, A의 전치 행렬은 \(A^T = \begin{bmatrix} a_{11}& a_{21}& a_{31} \\ a_{12}& a_{22} & a_{32} \\ a_{13}& a_{23} & a_{33} \\ a_{14}& a_{24} & a_{34} \\ \end{bmatrix}\) 로 표기한다.
연산량이 많을 때 기존 행렬을 대각 행렬 또는 단위 행렬로 변환하면 연산량을 현저히 줄일 수 있다. 연산량이 줄어들면 그만큼 알고리즘을 학습하는 시간도 줄며, 메모리 사용량 등의 시스템 자원도 줄일 수 있다.
이제 행렬의 덧셈, 뺄셈, 곱셈, 스칼라 곱셈에 대해 예제로 살펴보자. 행렬의 덧셈과 뺄셈은 각 행렬에 대응되는 행과 열의 원소끼리 더하거나 빼면 된다.
덧셈: \(\begin{bmatrix} 1& 0\\ 2& 0\\ 3& 0\\ \end{bmatrix}\) + \(\begin{bmatrix} 0& 4\\ 0& 5\\ 0& 6\\ \end{bmatrix}\) = \(\begin{bmatrix} 1& 4\\ 2& 5\\ 3& 6\\ \end{bmatrix}\)
뺄샘: \(\begin{bmatrix} 1& 4\\ 2& 5\\ 3& 6\\ \end{bmatrix}\) - \(\begin{bmatrix} 0& 3\\ 1& 4\\ 2& 5\\ \end{bmatrix}\) = \(\begin{bmatrix} 1& 1\\ 1& 1\\ 1& 1\\ \end{bmatrix}\)
행렬의 곱셈은 행렬 간의 곱셈을 포함한 여러 곱셈 중 스칼라 곱셈을 포함하고 있다. 스칼라 곱셈은 모든 행과 열의 원소에 스칼라 곱의 크기만큼 곱하면 된다.
예를 들어 앞서 A로 표현한 행렬에 3을 곱한 3A는 다음과 같이 표현할 수 있다.
3A = \(\begin{bmatrix} 3*a_{11} &3*a_{12} &3*a_{13} &3*a_{14} \\ 3*a_{21} &3*a_{22} &3*a_{23} &3*a_{24} \\ 3*a_{31} &3*a_{32} &3*a_{33} &3*a_{34} \\ \end{bmatrix}\)
행렬 간의 곱셈을 할 때에는 주의해야 할 점이 있다. 이는 곱셈이 되기 위한 필요 조건으로, 행렬 곱셈에서의 앞 행렬의 열의 크기와 뒤 행렬의 행의 크기가 일치해야 한다는 것이다.
A B = AB
2 * 3 3 * 4 2 * 4
딥러닝 알고리즘 최적화와 관련하여 자주 사용되는 행렬 간의 곱셈은 행렬의 원소곱이다. 이는 앞으로 딥러닝 관련 논문들을 읽을 때도 도움이 될 것이다.
행렬의 원소곱을 하기 위한 필요 조건은 곱하려는 두 행렬의 차원이 같아야 한다는 점이다. 두 행렬의 차원이 같다면, 각 행과 열의 원소끼리 서로 곱하면 된다.
A⊙B = \(\begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1}& \cdots & a_{mn}\\ \end{bmatrix}\) ⊙ \(\begin{bmatrix} b_{11} & \cdots & b_{1n} \\ \vdots & \ddots & \vdots \\ b_{m1}& \cdots & b_{mn}\\ \end{bmatrix}\)
A = \(\begin{bmatrix} 1& 1\\ 2& 2\\ 3& 3\\ \end{bmatrix}\), B = \(\begin{bmatrix} 1& 2\\ 2& 3\\ 3& 4\\ \end{bmatrix}\) 라 가정할 때, A⊙B = \(\begin{bmatrix} 1& 2\\ 4& 6\\ 9& 12\\ \end{bmatrix}\) 이다.
다음으로 알아볼 연산은 내적이다. 지금까지의 연산은 스칼라*스칼라=스칼라 또는 벡터*벡터=벡터였다면, 내적은 벡터*벡터=스칼라 값으로 표현된다. 내적의 표기는 <> 또는 dot(•)으로 나타낸다. 내적의 결과값은 벡터의 각 요소들 간의 곱셈 후 덧셈으로 구할 수 있다. 아래 예제를 살펴보자.
A = \(\begin{bmatrix} 1\\2 \end{bmatrix}\), B = \(\begin{bmatrix} 5\\6 \end{bmatrix}\) 이라 가정할 때, A•B = \(A^T\)•B = 1 * 5 + 2 * 6 = 17 이다.
내적을 알면 벡터 사이의 관계를 파악할 수 있다. 이는 앞으로 서포트 벡터 머신(SVM)을 공부할 때도 유용한데, 내적의 크기가 0이면(A•B=0) 두 벡터 사이의 각도가 90도라는 것만 알고 있자.
서포트 벡터 머신 외에도 주성분 분석(PCA)을 위해 특이값 분해를 할 수 있다. 특이값 분해를 이해하기 위해서 벡터 공간과 기저, 스팬, 랭크와 차원, 역행렬 등을 알아야 한다. 벡터 공간(Vector Space)이란 벡터 집합 중 특정 벡터들로 구성할 수 있는 공간을 일컫는다. 기저(Basis)란 벡터 공간을 구성하는 선형 벡터들을 말한다. 스팬(Span)은 쉽게 말하자면 벡터 공간의 부분 공간이다. 예를 들어 전체 벡터 공간 A가 4차원일 때, 그 공간 중 2개의 기저 벡터의 집합을 Q라 하자. 집합 Q의 두 기저 벡터들로 구성되는 2차원의 부분 공간을 B라 했을 때, B=span(A), B는 A의 부분 공간이라 표현한다.
벡터 공간과 기저를 이해하면 랭크와 차원을 이해하기 쉽다. 차원(Dimension)은 기저 벡터의 개수를 의미한다. 랭크(Rank)를 이해하기 앞서 열 공간과 행 공간을 먼저 소개하자면, 열 공간이란 열 벡터로 Span할 수 있는 공간을 말하고, 행 공간은 마찬가지로 행 벡터로 Span할 수 있는 공간을 말한다. 이때 랭크(Rank)란 3차원의 공간에서 존재하는 3개의 기저 벡터 중, 열 벡터로 인해 Span된 벡터 공간의 차원을 말한다.
역행렬의 의미는 간단하다. 행렬 ‘A’와 ‘B’를 곱했을 때 그 결과가 단위 행렬 ‘I’인 경우 행렬 ‘B’를 행렬 ‘A’의 ‘역행렬’이라 한다. 수식으로 표현하면 \(AA^{-1}\) 이다.
특이값 분해(Singular Value Decomposition, SVD)를 간단히 소개하면, 행렬 M는 \(V^*\), ∑, U 로 총 3번의 선형 변환을 거친다. 이를 시각화 한 아래 그림을 참조하자.
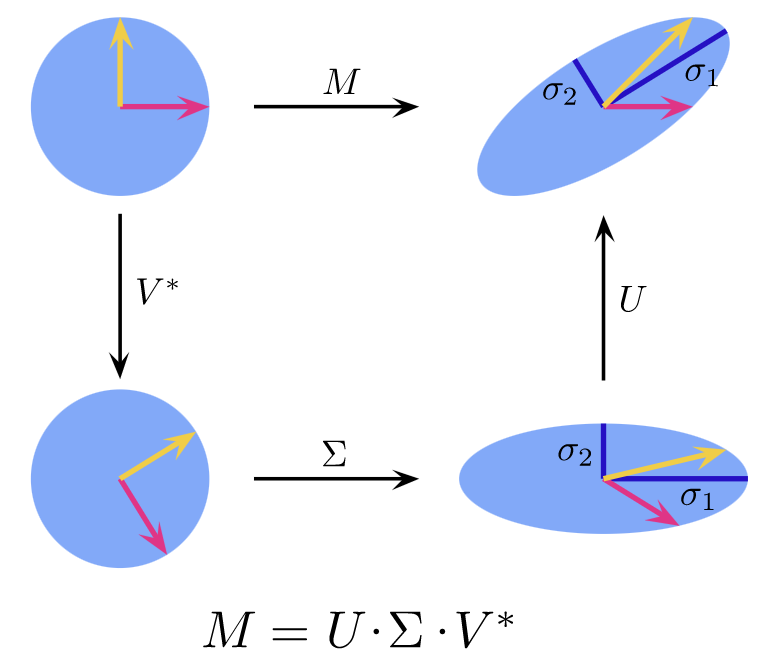
(특이값 분해, 이미지 출처: Wikipedia)
추후 Chapter 3-2에서 PCA와 특이값 분해에 대해 심층적으로 알아볼 것이다.
1-2. 평균과 분산
우리가 흔히 사용하는 시계열 데이터를 다루는 평균은 산술 평균(Mean)이다. 산술 평균은 전체 데이터 값의 합을 전체 데이터 개수로 나눈 것을 의미한다. 이때 데이터의 특징에 따라 모집단의 평균을 구할 수 있고 이를 모평균이라 한다. 모평균의 추정량을 표본 평균이라 한다.
분산(Variance)은 데이터가 얼마나 퍼져 있는지를 나타낸 것이다. 마찬가지로 데이터의 특징에 따라 모분산과 표본분산으로 나타낼 수 있다. 분산의 제곱근을 우리는 표준 편차(Standard deviation)라 한다. 머신러닝에서 우리는 평균과 분산을 자유롭게 머리속에 그릴 수 있어야 한다. 데이터의 중심은 평균, 데이터의 퍼진 정도를 분산이라 기억하며 데이터의 위치를 파악하면, 분포를 그려보지 않아도 된다.
공분산이란 무엇인가?
공분산(Covariance)이란 두 확률 변수 X, Y의 상관관계를 나타내는 값이다. 공분산이 양수일 때, 우리는 두 확률 변수 X와 Y가 양의 상관관계에 있다고 판단할 수 있다. 만약 두 확률 변수 X, Y가 서로 독립이면, 상관관계는 존재하지 않는다. 이때 공분산의 값은 0이다.
상관관계와 인과관계의 용어적 의미 차이를 잘 이해해야 한다. XAIOps의 분석기능에서도 찾아볼 수 있지만, 상관관계란 두 변수 간에 관계가 있다는 것을 의미한다. 이는 양의 상관관계 또는 음의 상관관계로 표현되는데, 수치의 절댓값이 1에 가까울수록 상관이 높다고 말한다. 인과관계란, 말 그대로 어떠한 원인으로 어떠한 결과가 있다는 원인과 결과의 관계를 의미한다. 따라서 우리가 다룰 시계열 데이터에서는 데이터 간의 시간적 차이가 있어야 인과관계를 설명할 수 있다. 인과관계는 상관관계가 필요 조건이다. 그러나 상관관계만으로는 인과관계를 설명하지 못하므로 인과관계는 상관관계의 충분조건이라 말할 수 있다.
1-3. 정규 분포
정규 분포(Normal distribution)는 통계학에서 가장 흔히 사용되는 기본적인 분포(연속형 확률 밀도 함수)이다. 예를 들어 동전을 N번 던졌을 때 앞이 나올 확률의 분포는 종모양의 정규분포를 따르며 인간을 포함한 다양한 생물종의 키는 종별로 정규분포를 따르고 있음을 발견할 수 있다.
시계열 데이터의 분포도 정규 분포를 따른다. 논문에서 주로 보듯, 가우시안 분포(Gaussian Distribution)라는 것은 정규 분포와 동일한 의미로 쓰인다. (수학자 가우스가 천문대 소장을 맡고 있을 때 천체 관측의 오차로서 나타나는 확률 분포를 분석하여 위와 같은 분포도를 도출했다고 한다.)

(정규 분포, 이미지 출처: freepik)
정규 분포는 위 그림과 같이 종 모양의 분포로 표현된다. 여기서 \(\mu\) (뮤)로 표현된 수식이 평균이며, 분산은 \(\sigma^2 \) (시그마 제곱)이다. 표준 정규 분포는 평균이 0, 분산이 1인 정규 분포를 의미한다. \(\mu\) 는 확률 분포의 평균치이며 \(\sigma^2 \) 는 분포의 흩어짐이나 퍼짐의 정도를 나타낸다. 정규분포에서 특정 조건을 충족할 확률은 해당 구간의 면적을 계산하면 된다.
이번 챕터에서는 기초 행렬부터 평균과 분산, 공분산, 상관관계, 인과관계, 정규 분포에 대해 알아보았다. 이러한 기초적인 통계학 지식은 앞으로 머신러닝을 다룰 때 많은 논문과 서적들에 등장하니, 추후에 부족한 부분이 있으면 더 찾아서 공부해 볼 필요가 있다.
다음 챕터에서는 Pandas에서 제공하는 Numpy와 Pandas라는 라이브러리를 활용하여 여러 실습 예제를 다룰 것이다. 실습 예제를 따라할 때, 행렬의 구조를 잘 떠올려보자.

기획 및 글 | AI 1팀 김경준

'엑셈 경쟁력 > 시계열 데이터처리 AI 알고리즘' 카테고리의 다른 글
| Chapter 2. Pandas 3편 : Time Series 머신러닝을 위한 Python 필수 라이브러리 (0) | 2022.08.25 |
|---|---|
| Chapter 2. Pandas 2편 : Time Series 머신러닝을 위한 Python 필수 라이브러리 (0) | 2022.08.25 |
| Chapter 2. Pandas 1편 : Time Series 머신러닝을 위한 Python 필수 라이브러리 (0) | 2022.08.25 |
| Chapter 2. Numpy 2편 : Time Series 머신러닝을 위한 Python 필수 라이브러리 (0) | 2022.07.27 |
| Chapter 2. Numpy 1편 : Time Series 머신러닝을 위한 Python 필수 라이브러리 (0) | 2022.07.27 |





댓글